|
|
| 1. |
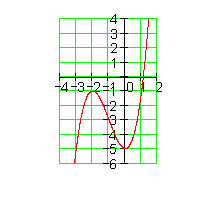
Gegeben ist der Graph einerganzrationalen Funktion 3. Grades.
Bestimmen Sie die Funktionsgleichung.
|
|
| |
Ausführliche Lösung
|
| |

Eine weitaus aufwendigere Methode wäre es gewesen, mit den Koordinaten von 4 aus dem Graphen abgelesenen Punkten ein Gleichungssystem aufzustellen und dieses mit dem Gauß- Algorithmus zu lösen.
|
| 2. |
Die Abbildung zeigt zwei Graphen ganzrationaler Funktionen 4. Grades.
Bestimmen Sie jeweils den Funktionsterm.
|

|
| |
Ausführliche Lösung
|
| |
f(x) hat bei x1 = -1 eine dreifache Nullstelle (Sattelpunkt) und bei x2 = 2 eine einfache Nullstelle. Außerdem verläuft der Graph durch P( 1 | -2 ).
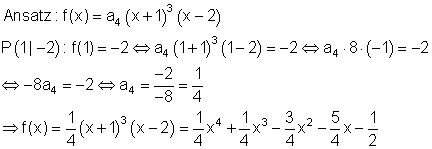
g(x) hat 4 Nullstellen:
x1 = -2 ; x2 = -1 ; x3 = 1 und x4 = 2 und schneidet die y- Achse bei y = -2
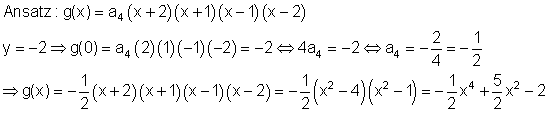
|
| 3. |

|

|
| |
Ausführliche Lösung
|
| |

Die Nullstelle liegt etwa bei x = 1,353
|
| 4. |

|
|
| |
Ausführliche Lösung
|
| |
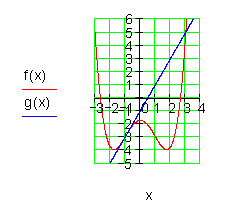
Die Schnittpunkte mit der Geraden werden aus der Grafik abgelesen. Ebenso der Schnittpunkt der Geraden mit der y- Achse.

|
|
|