In diesem Beitrag erkläre ich die Begriffe Erwartungswert, Varianz, Standardabweichung und binomialverteilte Zufallsgrößen. Außerdem stelle ich viele Beispiele dazu zur Verfügung.
- Beispiele von Binomialverteilungen für n = 40 und p variabel
- Erwartungswert einer binomialverteilten Zufallsgröße, Formel
- Varianz und Standardabweichung
- Link zu Aufgaben
Beispiele von Binomialverteilungen für n = 40 und p variabel
Wenn wir einen Bernoulli-Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,2 ist, n = 40 mal durchführen, erwarten wir im Mittel 8 Treffer.
Binomialverteilung für n = 40 und p = 0,2
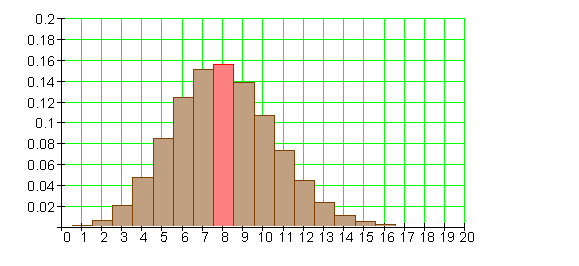
Führen wir einen Bernoulli-Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,4 ist,
n = 40 mal durch, dann erwarten wir im Mittel 16 Treffer.
Binomialverteilung für n = 40 und p = 0,4:
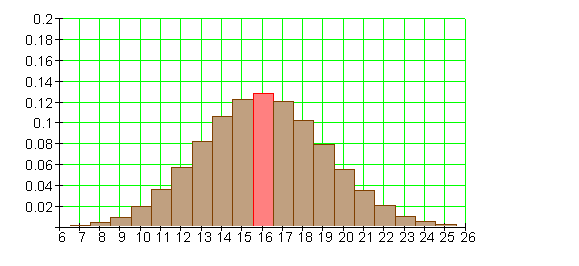
Führen wir einen Bernoulli-Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,5 ist,
n = 40 mal durch, dann erwarten wir im Mittel 20 Treffer.
Binomialverteilung für n = 40 und p = 0,5
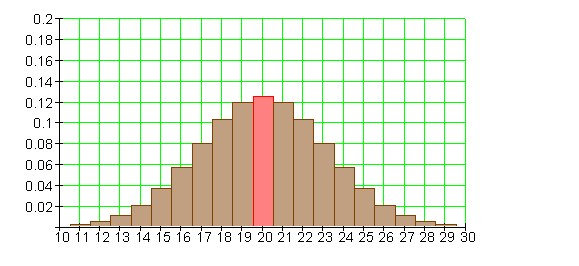
Wenn wir einen Bernoulli-Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,6 ist,
n = 40 mal durchführen, erwarten wir im Mittel 24 Treffer.
Binomialverteilung für n = 40 und p = 0,6
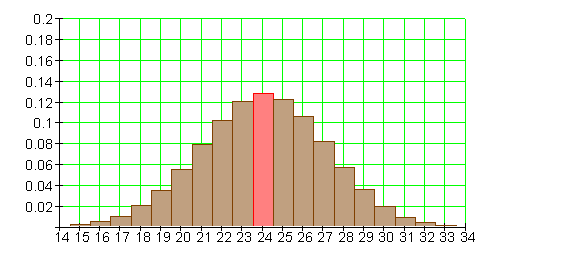
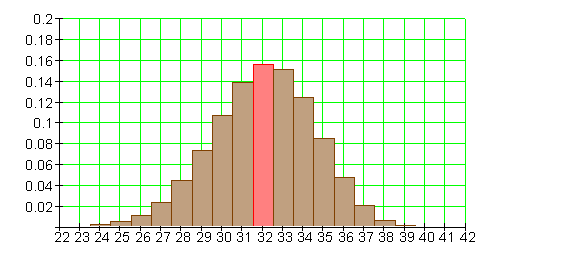
Führen wir einen Bernoulli-Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,8 ist,
n = 40 mal durch, dann erwarten wir im Mittel 32 Treffer.
Binomialverteilung für n = 40 und p = 0,8
Erwartungswert einer binomialverteilter Zufallsgröße
Beim Würfeln erwarten wir, dass bei 6000 Würfen die Zahl 6 etwa 1000 mal auftritt. Das bedeutet nicht, dass die Zahl 6 tatsächlich 1000 mal auftritt. Denn der Erwartungswert setzt unendlich viele Experimente voraus, deren Mittelwert er darstellt.
Mit anderen Worten:
Wenn wir einen Bernoulli-Versuch, bei dem die Trefferwahrscheinlichkeit p ist, n mal durchführen, dann erwarten wir im Mittel n mal p Treffer.
Erwartungswert einer Binomialverteilung

Den Beweis dazu stellen wir hier nicht vor. Man kann ihn mithilfe des Binomischen Lehrsatzes durchführen.
Beim Betrachten der Histogramme fällt auf, dass die mit der größten Wahrscheinlichkeit auftretenden Ergebnisse dem Erwartungswert entsprechen. Die Form der Histogramme ist dabei ähnlich. Sie entspricht der einer Glocke. Für p = 0,5 liegen die Werte symmetrisch zum Erwartungswert. Für p < 0,5 ist die Verteilung „linksschief“. Für p > 0,5 dagegen „rechtsschief“.
In der Nähe des Erwartungswertes liegen die Ergebnisse mit den höchsten Wahrscheinlichkeiten. Die Höhe einer Säule entspricht dabei der Wahrscheinlichkeit des zugehörigen Ergebnisses. Ihre Breite beträgt 1 Einheit. Da aber die Summe aller Einzelwahrscheinlichkeiten eines Zufallsexperimentes immer 1 ist, ergibt die Summe aller Säulenflächen ebenfalls den Wert 1. Die Fläche der Säulen in einem bestimmten Intervall ist somit ein Maß für die Wahrscheinlichkeit aller Erfolge, die in diesem Intervall liegen.
Varianz und Standardabweichung
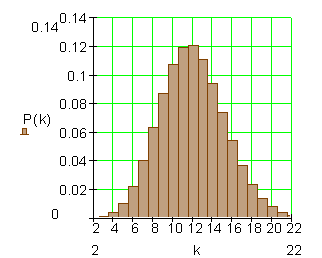
Binomialverteilung für n = 120 und p = 0,1
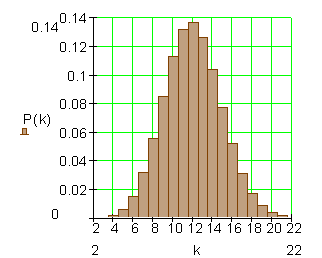
Binomialverteilung für n = 40 und p = 0,3
Beide Binomialverteilungen haben den gleichen Erwartungswert
![]()
![]()
Obwohl beide Verteilungen den gleichen Erwartungswert haben, sehen sie unterschiedlich aus. Wir untersuchen die Streuung um den Erwartungswert. Aus der beschreibenden Statistik ist die Varianz, bzw. die Standardabweichung als Streumaß bekannt.
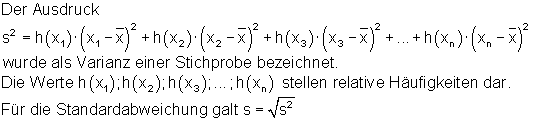
Entsprechend definieren wir für Wahrscheinlichkeitsverteilungen:
Varianz und Standardabweichung

Speziell für Binomialverteilungen gilt:
Varianz und Standardabweichung für Binomialverteilungen

Den Beweis führen wir hier ebenfalls nicht durch.


Bei der ersten Verteilung ist die Streuung etwas größer als bei der zweiten.

