Wenn wir einen Würfeln mehrmals werfen, hängt die Wahrscheinlichkeit eine bestimmte Zahl zwischen 1 und 6 zu werfen, nicht von dem vorherigen Ergebnis ab. Denn jeder Wurf geschieht unabhängig von dem vorigen.
Wenn man jedoch aus einer Urne mit verschieden farbigen Kugeln nacheinander Kugeln zieht, ohne sie zurückzulegen, ist die Wahrscheinlichkeit für ein bestimmtes Ergebnis oft von dem vorigen Ergebnis abhängig.
Deshalb spricht man von einer bedingten Wahrscheinlichkeit.
Einführungsbeispiel bedingte Wahrscheinlichkeit
Z. B.: Eine Urne enthält 100 Kugeln. Davon bestehen 70 Kugeln aus dem Holz und 30 Kugeln aus Kunststoff. Außerdem sind 25 der Holzkugeln rot und 45 grün. Schließlich sind 10 der Kunststoffkugeln rot und 20 grün.
Wir definieren also folgende Ereignisse:
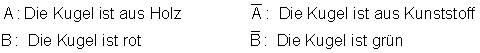
Die Kugeln tragen zwei Merkmale mit jeweils zwei Ausprägungen.
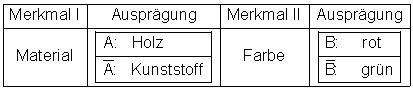
Dieser Sachverhalt können wir also in einer Vierfeldertafel darstellen:

Dann ziehen wir zufällig eine Kugel.
Mit den Daten der Tafel können wird danach folgende Wahrscheinlichkeiten berechnen:
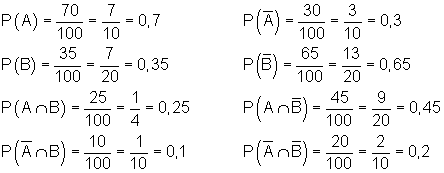
Dazu die Vierfeldertafel:
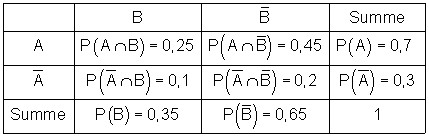
Wenn jemand eine Kugel zieht und spürt, dass es sich um eine Kunststoffkugel handelt. Wie groß ist die Wahrscheinlichkeit dafür, dass die Kugel grün ist?
Das ist allerdings nicht die Wahrscheinlichkeit, mit der man eine grüne Kunststoffkugel zieht. Aus der Vierfeldertafel lässt sich die gesuchte Wahrscheinlichkeit deshalb nicht ablesen.
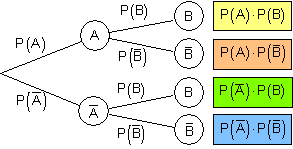
Mit einem Ereignisbaum können wir jedoch diese Frage klären:
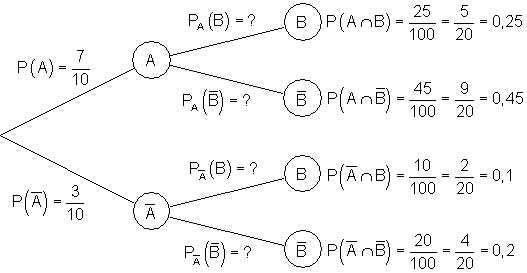
Die Bezeichnung PA(B) bedeutet: Die Wahrscheinlichkeit von B unter der Bedingung, dass A bereits eingetreten ist.
Diese Wahrscheinlichkeit nennen wir deshalb bedingte Wahrscheinlichkeit.
![]()
In Worten:
Wie groß ist die Wahrscheinlichkeit, eine grüne Kugel zu ziehen, wenn man weiß, dass die gezogene Kugel aus Kunststoff ist?
Wir suchen also nach einer Wahrscheinlichkeit, die von einer Bedingung abhängt.
In diesem Fall lautet die Bedingung: Die gezogene Kugel ist aus Kunststoff.
Um die im Baumdiagramm noch fehlenden Wahrscheinlichkeiten auszurechnen, verwendet man die Pfadmultiplikationsregel:
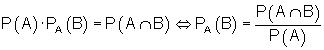
Der englische Mathematiker Thomas Bayes (1702 – 1761) hat die Regel entwickelt, nach der die bedingte Wahrscheinlichkeit berechnet wird. Deshalb nennt man sie auch Bayes’sche Regel oder Satz von Bayes.
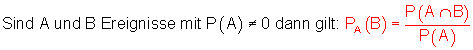

Wenn man weiß, dass die gezogene Kugel aus Kunststoff besteht, ist die Wahrscheinlichkeit, dass sie die Farbe grün hat: 2/3. Die Wahrscheinlichkeit eine grüne Kunststoffkugel zu ziehen ist hingegen 0,2.
Ein etwas anderer Zugang zur bedingten Wahrscheinlichkeit:
Eine Urne enthält 3 grüne und 2 rote Kugeln.
Wir ziehen nacheinander zwei Kugeln ohne Zurücklegen.
Dann definieren wir vier Ereignisse:
A: Grün wird im 1. Zug gezogen.
B: Grün wird im 2. Zug gezogen.
C: Grün wird im ersten und zweiten Zug gezogen.
D: Grün im zweiten Zug, wenn grün bereits im ersten Zug gezogen wurde.
Zuerst bestimmen wir die Wahrscheinlichkeiten aller Ereignisse:
Ein Baumdiagramm mit den Pfadwahrscheinlichkeiten veranschaulicht den Zusammenhang.
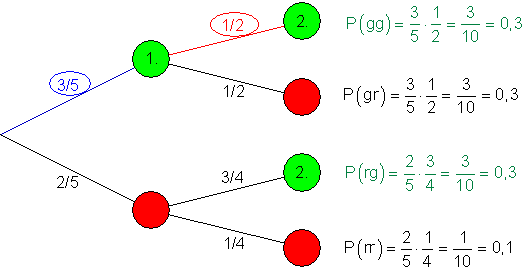

Den Wert von P(D) ermitteln wir dabei so:
Unter der Voraussetzung (Bedingung) dass im 1. Zug grün gezogen wurde, weiß man, dass noch 2 grüne und 2 rote Kugeln in der Urne sind.
Die Wahrscheinlichkeit für grün im 2. Zug ist deshalb 1/2.
Für die Wahrscheinlichkeit von D (grün im 2. Zug) unter der Voraussetzung dass A (grün im 1. Zug) schon eingetreten ist, wählt man die Bezeichnung P(D) = PA(B).
![]()
Schauen wir uns danach den Ausschnitt an in dem Pfaddiagramm an, in dem PA(B) vorkommt.
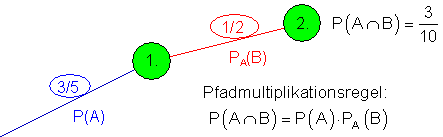
Wenn man nach der Wahrscheinlichkeit PA(B), so kann man obige Gleichung wie folgt umformen:
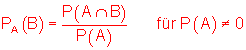
PA(B) ist die Wahrscheinlichkeit von B unter der Bedingung, dass A bereits eingetreten ist.
Wir überprüfen dieses Gesetz mit den vorliegenden Ergebnissen:
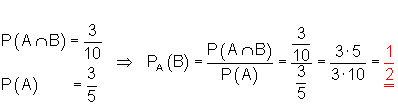
Aus dem Urnenversuch (mehrfaches ziehen ohne zurücklegen) geht klar hervor, das die Wahrscheinlichkeit für die jeweils nächste Ziehung von der vorigen abhängt.
Mit anderen Worten: die Ereignisse sind voneinander abhängig.
Unabhängigkeit von Ereignissen
Bei einem Urnenversuch (mehrfaches ziehen mit Zurücklegen), stellen wir die Anfangsbedingung immer wieder so her, dass die Wahrscheinlichkeit für die jeweils nächste Ziehung genauso ist wie bei der ersten.
Anders ausgedrückt: die Ereignisse sind voneinander unabhängig.
Zum Beispiel: eine Urne enthält 3 grüne und 2 rote Kugeln.
Wir ziehen nacheinander zwei Kugeln mit Zurücklegen.
Dann definieren wir vier Ereignisse:
A: Grün wird im 1. Zug gezogen.
B: Grün wird im 2. Zug gezogen.
C: Grün wird im ersten und zweiten Zug gezogen.
D: Grün im zweiten Zug unter der Bedingung, dass grün bereits im ersten Zug gezogen wurde.
Dazu das Baumdiagramm mit den zugehörigen Pfadwahrscheinlichkeiten:
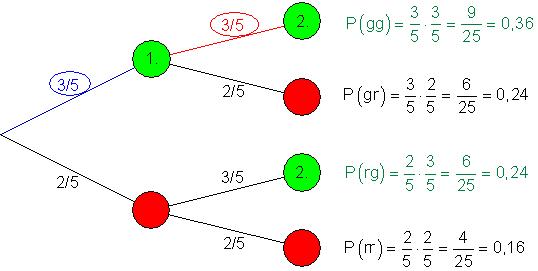

Die Wahrscheinlichkeit eine grüne Kugel zu ziehen, bleibt immer gleich. Denn nach jedem Zug wird durch Zurücklegen der Kugel die Ausgangssituation wieder hergestellt.
Die Wahrscheinlichkeit für grün im 2. Zug unter der Bedingung, dass grün im 1. Zug bereits gezogen wurde, ist P(D) = PA(B).
Schauen wir uns hierzu einen Ausschnitt aus dem Baumdiagramm an:
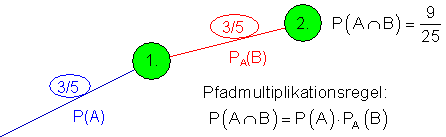

Wenn PA(B) = P(B) gilt, so beeinflusst das Eintreten des Ereignisses A die Wahrscheinlichkeit von B nicht.
Mit anderen Worten: die Ereignisse A und B sind unabhängig voneinander.
Definition: Unabhängige Ereignisse:
Das Ereignis B heißt unabhängig vom Ereignis A, wenn das Eintreten von A die Wahrscheinlichkeit für das Eintreten von B nicht beeinflusst.
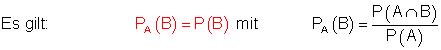
Wenn wir z. B. aus einer Urne ziehen mit Zurücklegen.
Unabhängigkeit zweier Ereignisse nachweisen:
Wenn man die Unabhängigkeit zweier Ereignisse nachweisen will, geht man wie folgt vor:

Dann sind die Ereignisse A und B voneinander unabhängig. Andernfalls sind die Ereignisse A und B voneinander abhängig. Im Baumdiagramm erkennt man die Unabhängigkeit von Ereignissen daran, dass in der 2. Stufe die Teilbäume gleich sind. Sind sie hingegen verschieden, dann sind die Ereignisse voneinander abhängig.
Beispiel 1 für bedingte Wahrscheinlichkeit
Wir färben die Seitenflächen eines idealen Würfels wie folgt ein:
Zwei Seitenflächen rot und zwei grün. Eine Seitenfläche mit der Farbe schwarz und eine mit der Farbe blau.
Dann werfen wir den Würfel zweimal. Daraufhin definieren wir folgende Ereignisse:
A: Beim ersten Wurf erscheint die Farbe rot oder schwarz.
B: Beim zweiten Wurf erscheint die Farbe grün oder blau.
Untersuche, ob die Ereignisse A und B voneinander unabhängig sind!
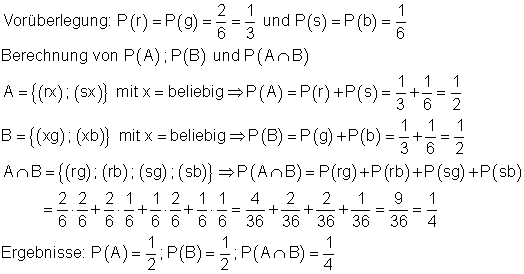
Zwei Ereignisse A und B sind unabhängig voneinander, wenn gilt:
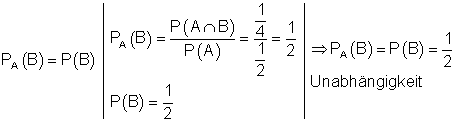
Die Ereignisse A und B sind also unabhängig voneinander.
Die Zusammenhänge betrachten wir an einer 4-Feldertafel und dem zugehörigen Baumdiagramm. Bekannt ist dabei:
![]()
Daraus können wir anschließend die restlichen Werte für die 4-Feldertafel berechnen.
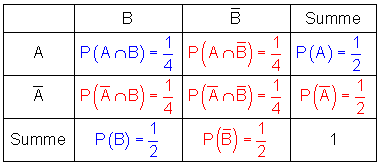
Für das Baumdiagramm benötigen wir alle bedingten Wahrscheinlichkeiten. Diese können wir leicht mit den Werten der 4-Feldertafel berechnen.
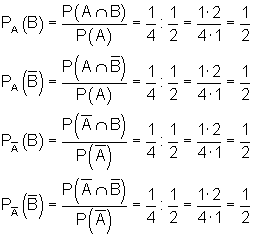
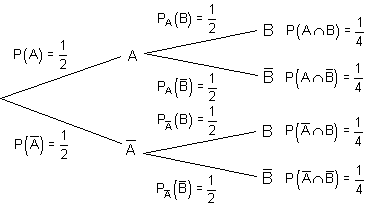
Der Vergleich mit der 4-Feldertafel zeigt, dass alle Ereignisse unabhängig voneinander sind, denn es gilt.
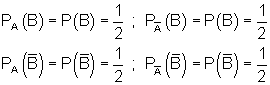
Man erkennt die Unabhängigkeit der Ereignisse voneinander auch daran, dass in der 2. Stufe des Baumdiagramms die Teilbäume gleich sind.
Beispiel 2 für bedingte Wahrscheinlichkeit
Ein Würfel in Form einer dreieckigen Pyramide hat 4 gleich große Flächen mit den Zahlen 1 ; 2 ; 3; 4. Mit anderen Worten: ein 4-er Würfel.
Wir werden den Würfel zweimal. Dann definieren wir folgende Ereignisse:
A: Beim 1. Wurf erscheint die Zahl 1 oder 2 und beim 2. Wurf die Zahl 1 ; 2 oder 4.
B: Die Zahl beim 2. Wurf ist eine andere als beim 1. Wurf.
Untersuche, ob die Ereignisse A und B voneinander unabhängig sind!
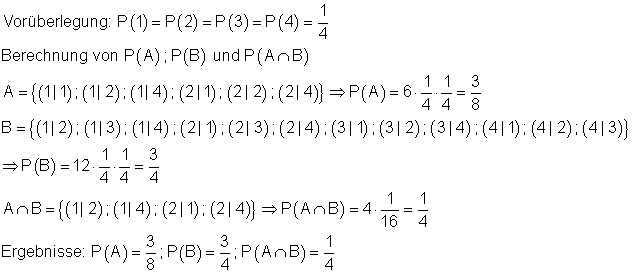
Zwei Ereignisse A und B sind unabhängig voneinander, wenn gilt:
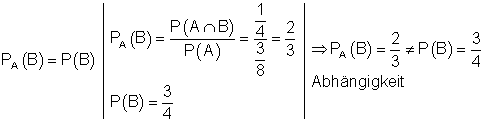
Die Ereignisse A und B sind also voneinander abhängig.
Die Zusammenhänge betrachten wir nun an einer 4-Feldertafel und dem zugehörigen Baumdiagramm. Bekannt dazu ist:
![]()
Daraus können wir die restlichen Werte für die 4-Feldertafel berechnen.

Für das Baumdiagramm benötigen wir alle bedingten Wahrscheinlichkeiten. Diese können wir leicht mit den Werten der 4-Feldertafel berechnen.
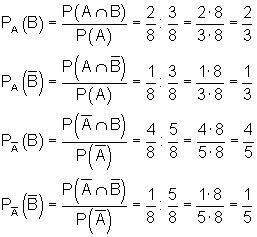
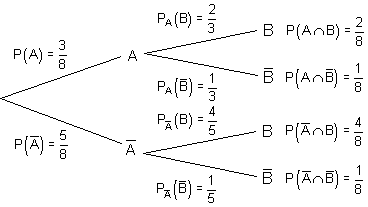
Der Vergleich mit der 4-Feldertafel zeigt, dass alle Ereignisse abhängig voneinander sind, denn es gilt:
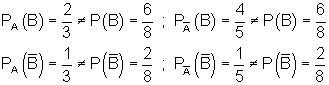
Man erkennt die Abhängigkeit der Ereignisse voneinander auch daran, dass in der 2. Stufe des Baumdiagramms die Teilbäume ungleich sind.
Beispiel 3 für bedingte Wahrscheinlichkeit
Eine Umfrage an Schulen über die Essgewohnheiten der Schüler hat ergeben, dass 45% aller Schüler gerne Schokolade essen.
55% aller Schüler ziehen andere Süßigkeiten vor.
60% aller Schüler gaben an Geschwister zu haben.
27% der Schüler haben Geschwister und essen gerne Schokolade.
Ein Schokoladenhersteller interessiert sich dafür, ob Schüler mit Geschwister eine besondere Vorliebe für Schokolade haben.
Anders ausgedrückt: Hat die Tatsache, das ein Schüler Geschwister hat, einen Einfluss auf seine Vorliebe für Schokolade?
Die Erhebungsdaten können wir in einer Vierfeldtafel darstellen.
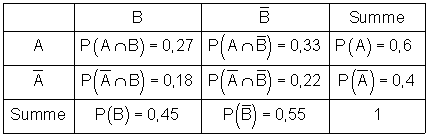
Die zugehörigen Ereignisse sind:
A: Der Schüler hat Geschwister.
B: Der Schüler isst gerne Schokolade.
Wir überprüfen dies auf Abhängigkeit:
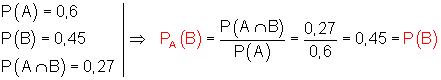
Die Ereignisse sind also unabhängig voneinander.
Anders ausgedrückt: ob ein Schüler Geschwister hat oder nicht, hat keinen Einfluss auf seine Vorliebe für Schokolade.
Die Zusammenhänge betrachten wir nun an dem zugehörigen Baumdiagramm. Für das Baumdiagramm benötigen wir nn alle bedingten Wahrscheinlichkeiten. Diese können wir wieder leicht mit den Werten der 4-Feldtafel berechnen.
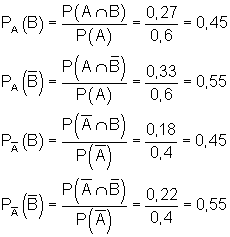
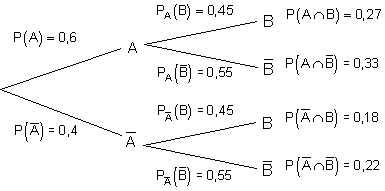
Der Vergleich mit der 4-Feldtafel zeigt, dass alle Ereignisse unabhängig voneinander sind, denn es gilt:

Man erkennt die Unabhängigkeit der Ereignisse voneinander auch daran, dass in der 2. Stufe des Baumdiagramms die Teilbäume gleich sind.
Beispiel 4 für bedingte Wahrscheinlichkeit mit Vierfeldertafel und Baumdiagramm
Ein Berufskolleg hat 1000 Schüler. Die folgende Vierfeldtafel gibt Aufschluss darüber, wie die Handys auf die Schüler verteilt sind.

a) Berechne die relativen Häufigkeiten und trage diese in eine neue Vierfeldtafel ein!
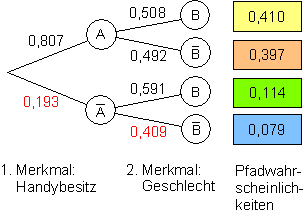
b) Benutze den Zusammenhang zwischen einer Vierfeldtafel und den Baumdiagrammen um die Bäume zu zeichnen.
c) Berechne alle bedingten Wahrscheinlichkeiten und trage diese in die Baumdiagramme ein!
d) Dann wählen wir aus allen Schülern einen zufällig aus.
1) Mit welcher Wahrscheinlichkeit hat die Person kein Handy?
2) Mit welcher Wahrscheinlichkeit ist die Person weiblich?
3) Falls eine ausgewählte Person kein Handy hat, mit welcher Wahrscheinlichkeit ist sie männlich?
4) Falls eine ausgewählte Person weiblich ist, mit welcher Wahrscheinlichkeit hat sie ein Handy?
5) Besteht ein Zusammenhang zwischen Geschlecht und Handybesitz?
Lösungen:
a)
| Summe | |||
| 0,410 | 0,397 | 0,807 | |
| 0,114 | 0,079 | 0,193 | |
| Summe | 0,524 | 0,476 | 1 |
b)
![]()
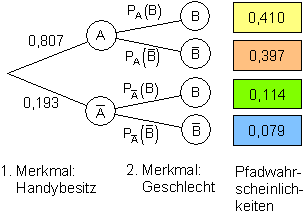
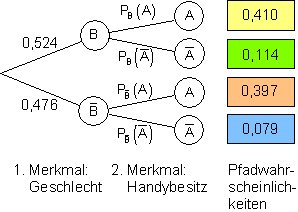
c) Wir berechnen die bedingte Wahrscheinlichkeiten: Wir lesen die Wahrscheinlichkeiten aus der Vierfeldtafel ab und ordnen sie den Ereignissen zu:
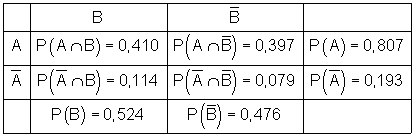
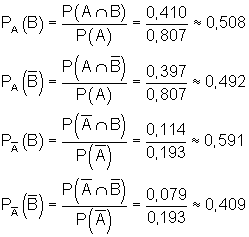
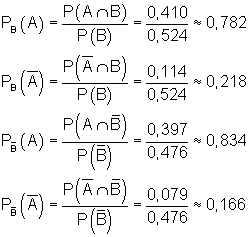
![]()
![]()
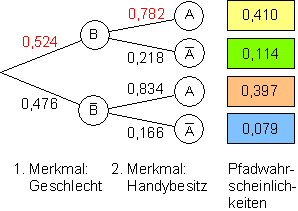
d) Die gesuchten Wahrscheinlichkeiten können wir nun direkt aus den Baumdiagrammen ablesen.
1.) ![]()
Eine zufällig ausgewählte Person hat mit einer Wahrscheinlichkeit von 0,193 kein Handy.
2.) ![]()
Eine zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von 0,524 weiblich.
3.) ![]()
Eine zufällig ausgewählte Person, von der man weiß, dass sie kein Handy hat, ist mit einer Wahrscheinlichkeit von 0,409 männlich.
4.) ![]()
Eine zufällig ausgewählte Person, von der man weiß, dass sie weiblich ist, hat mit einer Wahrscheinlichkeit von 0,782 ein Handy.
5.) Wir überprüfen auf Abhängigkeit. (Zusammenhang zwischen Geschlecht und Handybesitz):
![]()
Anderenfalls sind die Ereignisse voneinander abhängig.
Mit den bereits vorliegenden Ergebnissen lässt sich zeigen:
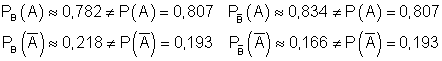
Folglich besteht in allen Fällen eine Abhängigkeit zwischen Geschlecht und dem Handybesitz.
Aus den Baumdiagrammen können wir die Abhängigkeit der Ereignisse direkt ablesen. Denn die Teilbäume der 2. Stufe sind verschieden.
Hat man den Zusammenhang einer Vierfeldtafel mit den Baumdiagrammen begriffen, dann lassen sich solche Aufgaben auch mit weniger Aufwand lösen. Das zeigt das nun folgende Beispiel.
Beispiel 5 für bedingte Wahrscheinlichkeit
Viele Internetnutzer klagen über Spam-Mails. Nehmen wir an, in 1% der guten und 40% der Spam- Mails komme das Wort „Viegro“ vor. Außerdem seien 10% der Mails gut und 90% Spam.
Wie groß ist die Wahrscheinlichkeit, dass eine Mail, von der man weiß, das in ihr das Wort „Viegro“ vorkommt, eine Spam-Mail ist?
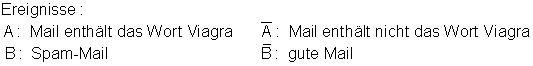
Dazu stellen wir die Vierfeldtafel mit den vorgegebenen Daten auf.
Die % Werte entsprechen dann den relativen Häufigkeiten (Wahrscheinlichkeiten).
90 % Spam bedeutet Summe Spam = 0,9
10% gute Mails bedeutet Summe gute Mails = 0,1
40% der Spam-Mails mit Viegro bedeutet 0,9 x 0,4 = 0,36
1% der guten Mails mit Viegro bedeutet =0,1 x 0,01 = 0,001
Die restliche Werte kann man dann ausrechnen, da die Summen bekannt sind.
| Summe | |||
| 0,36 | 0,001 | ||
| Summe | 0,9 | 0,1 | 1 |
| Spam ohne Viegro Gute Mail ohne Viegro: Summe aller Mails mit Viegro: Summe aller Mails ohne Viegro: |
0,9 – 0,36 = 0,54 0,1 – 0,001 = 0,099 0,36 + 0,001 = 0,361 0,54 + 0,099 = 0,639 |
Mit diesen Werten vervollständigen wir die Vierfeldtafel:
| Summe | |||
| 0,36 | 0,001 | 0,361 | |
| 0,54 | 0,099 | 0,639 | |
| Summe | 0,9 | 0,1 | 1 |
Wie groß ist die Wahrscheinlichkeit, dass eine Mail, in der Viegro“ steht, Spam ist?
Gesucht ist also die Wahrscheinlichkeit von B unter der Bedingung, dass A eingetreten ist.
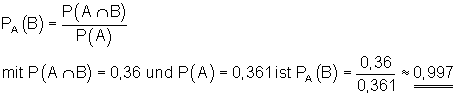
Das bedeutet also, in 99,7% aller Fälle ist eine Mail, in der Viegro steht, eine Spam-Mail.
Übung für bedingte Wahrscheinlichkeit:
Die Tabelle zeigt Frauen und Männer einer Firma, unterteilt in Raucher und Nichtraucher.

a) Berechne die Wahrscheinlichkeit, eine Person anzutreffen, die Raucher ist.
b) Berechne die Wahrscheinlichkeit eine Frau anzutreffen.
c) Berechne die Wahrscheinlichkeit eine Raucherin anzutreffen.
d) Wenn man eine Frau antrifft, mit welcher Wahrscheinlichkeit ist sie Raucherin?
e) Überprüfe, ob die Ereignisse A und B voneinander abhängig sind.
Die Lösung hierzu ist unten.
Zusammenfassung Bedingte Wahrscheinlichkeit:
Wenn Ereignis A bereits eingetreten ist, tritt Ereignis B mit folgender Wahrscheinlichkeit ein:
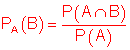
Unabhängige Ereignisse:
Das Ereignis B heißt unabhängig vom Ereignis A, wenn das Eintreten von A die Wahrscheinlichkeit für das Eintreten von B nicht beeinflusst.
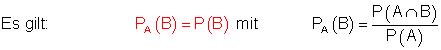
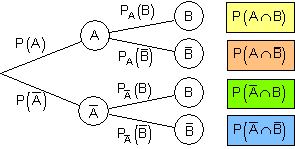
Zusammenhang zwischen Vierfeldtafel und Baumdiagramm
Vierfeldtafel
| 1 |
Baumdiagramm
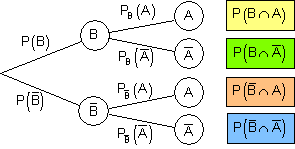
Wenn man bei einem Baumdiagramm die Reihenfolge der betrachteten Ereignisse vertauscht, erhält man das umgekehrte oder inverse Baumdiagramm. Die Wahrscheinlichkeiten an den Pfadenden stimmen in beiden Baumdiagrammen bis auf die Reihenfolge überein. Die Pfadwahrscheinlichkeiten und damit auch die bedingten Wahrscheinlichkeiten unterscheiden sich im Allgemeinen voneinander. Sie beziehen sich auf verschiedene Ereignisse und daher auch auf verschiedene Teilgesamtheiten. Beachte aber:
![]()
Umgekehrte Vierfeldtafel
| 1 |
Umgekehrtes Baumdiagramm
Vierfeldtafel und Baumdiagramm bei stochastischer Unabhängigkeit
Bei stochastisch unabhängigen Ereignissen A und B steht im ersten Feld der Vierfeldtafel für
![]() .
.
Für die weiteren Felder gilt entsprechend einer Multiplikationstabelle ähnliches.
Im Baumdiagramm erkennt man die Unabhängigkeit von Ereignissen daran, dass in der 2. Stufe die Teilbäume gleich sind.
Vierfeldtafel
| 1 |
Baumdiagramm
Lösung der Übung:
Die Tabelle zeigt Frauen und Männer einer Firma, unterteilt in Raucher und Nichtraucher.

a) Berechne die Wahrscheinlichkeit, eine Person anzutreffen, die Raucher ist!
b) Berechne die Wahrscheinlichkeit eine Frau anzutreffen!
c) Berechne die Wahrscheinlichkeit eine Raucherin anzutreffen!
d) Wenn man eine Frau trifft, mit welcher Wahrscheinlichkeit ist sie Raucherin?
e) Überprüfe, ob die Ereignisse A und B voneinander abhängig sind!
Lösung: Wenn wir die Wahrscheinlichkeiten bestimmen wollen, benötigen wir die relativen Häufigkeiten der Ereignisse. Im vorigen Beispiel gab es Rundungsfehler. Damit man diese vermeidet, sollte man die relativen Häufigkeiten und die dazugehörigen Wahrscheinlichkeiten in Bruchform darstellen.
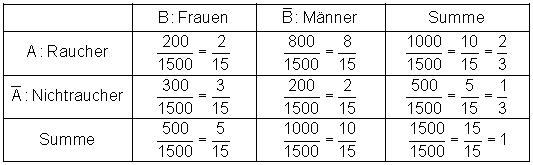
a) Die Wahrscheinlichkeit dafür, eine Person anzutreffen, die Raucher ist, beträgt
![]()
b) Die Wahrscheinlichkeit dafür, eine Frau anzutreffen, beträgt also:
![]() .
.
c) Die Wahrscheinlichkeit dafür, eine Raucherin anzutreffen, beträgt folglich
![]() .
.
d) Die Wahrscheinlichkeit dafür, dass eine angetroffene Frau Raucherin ist, beträgt demnach
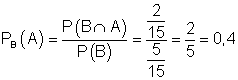 .
.
e) Zwei Ereignisse A und B sind unabhängig voneinander, wenn gilt:
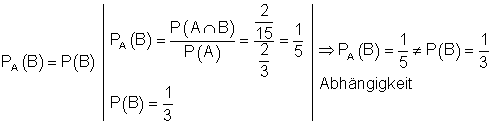 .
.
Die Ereignisse A und B sind also voneinander abhängig.
Dazu findest du hier Aufgaben.
Außerdem hier Aufgaben Bedingte Wahrscheinlichkeiten II.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung. Darin auch Links zu Aufgaben.