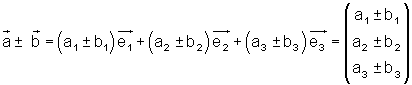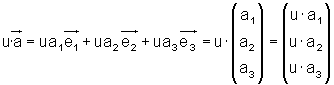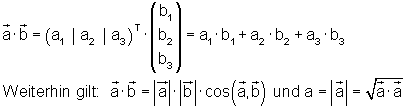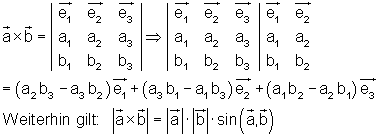In diesem Beitrag fasse ich noch einmal alle Rechengesetze für Vektoren zusammen.
Vektorregeln für die Addition und Subtraktion
Man addiert Vektoren, bzw. subtrahiert sie, indem man die einander entsprechenden Komponenten addiert bzw. subtrahiert, ausführlicher hier.
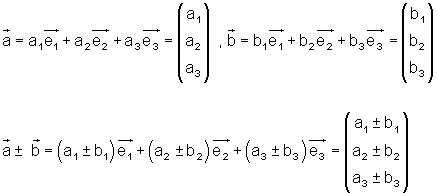
Beispiel Vektorregeln Addition, Subtraktion:
Gegeben sind die drei Vektoren:
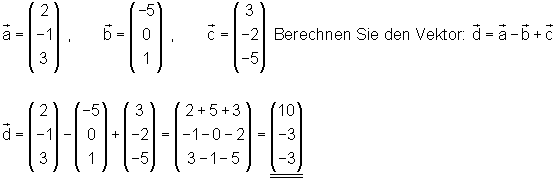
Vektorregel für die Multiplikation eines Vektors mit einem Skalar
Bei der Multiplikation eines Vektors mit einem Skalar, multipliziert man alle Komponenten des Vektors mit dem Skalar.
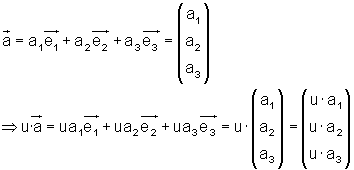
1. Beispiel Vektorregel für die Multiplikation eines Vektors mit einem Skalar:
Gegeben sind die drei Vektoren:
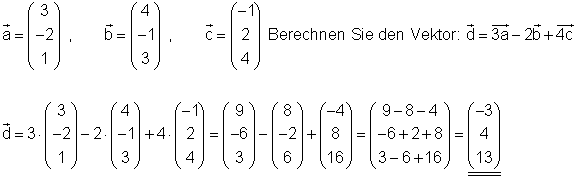
2. Beispiel Vektorregel für die Multiplikation eines Vektors mit einem Skalar:
Der Abstand zweier Punkte P1 und P2 im dreidimensionalen Raum soll bestimmt werden.
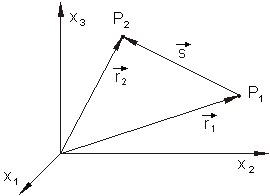
Die Ortsvektoren zu den Punkten sind:

Der Betrag des Verbindungsvektors beider Punkte entspricht ihrem Abstand voneinander im dreidimensionalen Raum.
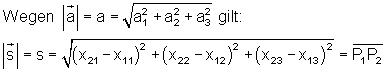
Bemerkung: Bei der Indizierung der Koordinaten xij steht der erste Index für den Punkt Pi und der zweite Index für die Koordinatenachse.
Vektorregeln für das Skalarprodukt
Siehe auch hier.
Gegeben seien die beiden Vektoren
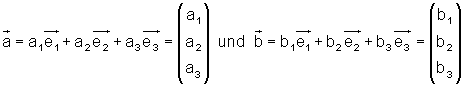
Diese multiplizieren wir zuerst formal miteinander:
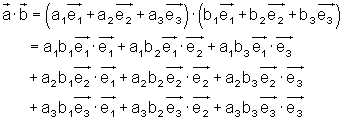
Wenn man beachtet, dass für zwei senkrecht aufeinanderstehender Vektoren das Skalarprodukt Null und das Quadrat eines Einheitsvektors 1 ist, vereinfacht sich oben stehender Ausdruck sehr.
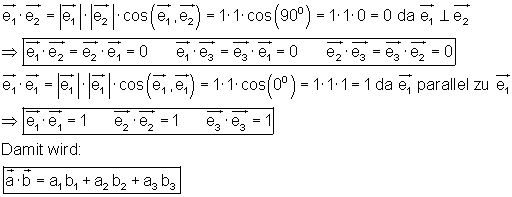
Die Skalarmultiplikation kann man auch mit Spaltenvektoren durchführen:
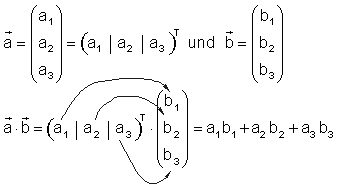
Beispiel Vektorregel für das Skalarprodukt:
Welchen Winkel schließen beide Vektoren miteinander ein?
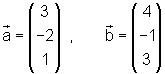
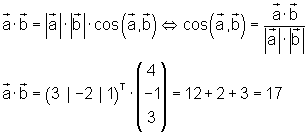
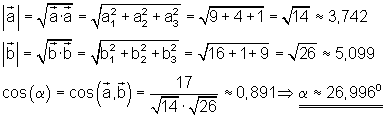
Vektorregeln für das vektorielle Produkt
Siehe auch hier.
Ähnlich wie beim skalaren Produkt multipliziert man zuerst formal. Danach vereinfacht man. Dazu sollte man sich die Regeln für das Kreuzprodukt noch mal ansehen.
Es gilt:

Für die Basisvektoren des kartesichen Koordinatensystems gilt insbesondere:

Formale Multiplikation:
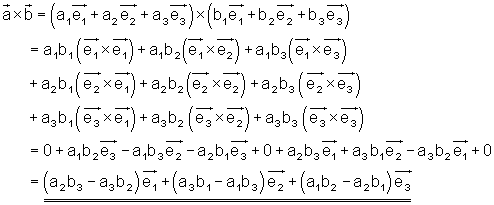
Den Aufbau der Formel kann man als dreireihige Determinante darstellen. Diese kann man nach der Regel von Sarrus berechnen, so dass sie die Berechnungsformel liefert. Wenn man die Regel von Sarrus anwendet, schreibt man zunächst die erste und die zweite Spalte noch einmal hinter die Determinante. Anschließend bildet man alle diagonalen Verbindungen dreier Elemente und zwar 3 mal von links oben nach rechts unten. Außerdem 3 mal von links unten nach rechts oben. Danach bildet man Produkte dieser jeweils drei Faktoren. Die so entstandenen Produkte fasst man anschließend zu einer Summe zusammen und zwar derart, dass man die Produkte von links oben nach rechts unten positiv und die von links unten nach rechts oben negativ zählen.
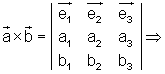
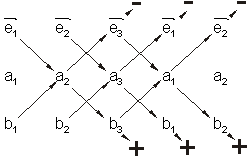
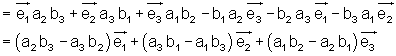
Beispiel Vektorregeln für das vektorielle Produkt:
Gegeben sind die Vektoren
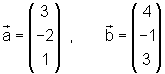
Das vektorielle Produkt aus beiden Vektoren soll gebildet werden. Das Ergebnis ist mit einer geeigneten Rechnung zu überprüfen.
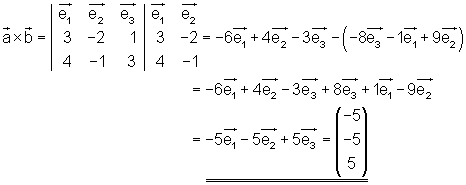
Die Probe kann man anschließend mit dem skalaren Produkt durchführen. Das Kreuzprodukt beider Vektoren ist ein Vektor, der senkrecht zu der Ebene liegt, die man von den beiden Vektoren aufspannt. Demzufolge muss das skalare Produkt des Ergebnisvektors mit beiden Vektoren den Wert Null ergeben.
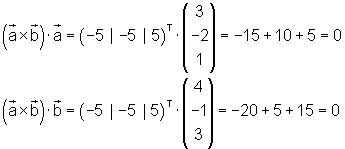
Beispiel Vektorregeln für das vektorielle Produkt:
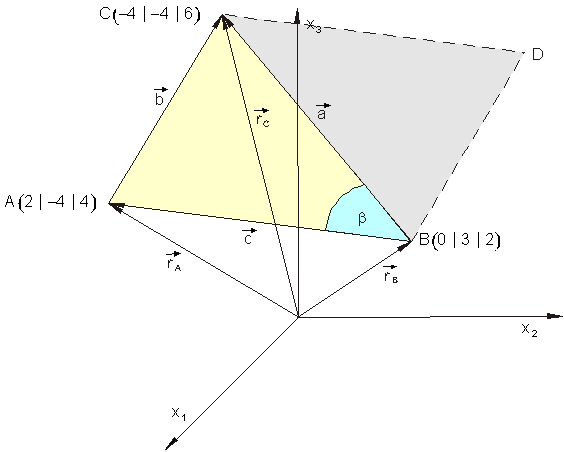
Die Eckpunkte A, B und C eines Dreiecks haben die Koordinaten
A( 2 | -4 | 4 ); B( 0 | 3 | 2 ) und C( -4 | -4 | 6 ).
Der Flächeninhalt des Dreiecks ist zu berechnen. Danach sollte man das Ergebnis ist mit den Formeln der ebenen Trigonometrie überprüfen.
Vorüberlegung: Eine Zeichnung zeigt die geometrische Darstellung.
Das Kreuzprodukt zweier Vektoren ist ein Vektor, der senkrecht zu der Ebene verläuft, die von den beiden Vektoren aufgespannt wird und dessen Betrag dem Flächeninhalt des Parallelogramms entspricht, das sich aus den beiden Vektoren bilden lässt. Die Diagonalen des Parallelogramms teilen dieses in jeweils zwei deckungsgleiche Dreiecke auf. Damit ist die Dreiecksfläche die Hälfte des Betrages vom Kreuzprodukt.
Die Ortsvektoren und die Vektoren der Dreiecksseiten werden ermittelt:
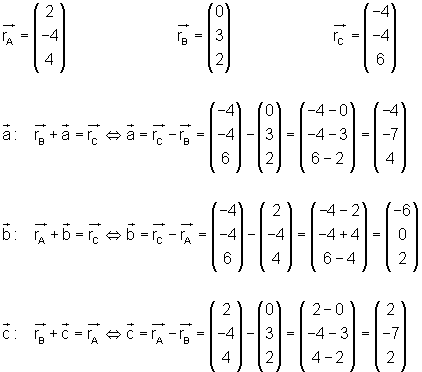
Die Fläche des eingezeichneten Parallelogramms erhält man über das Kreuzprodukt:
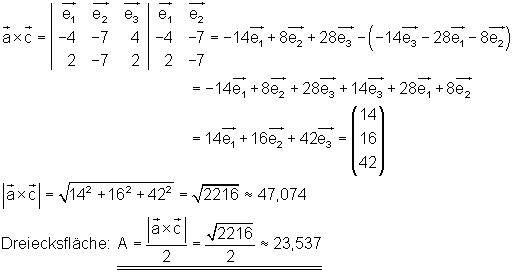
Ergebniskontrolle:
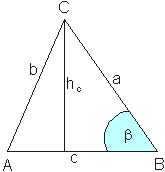
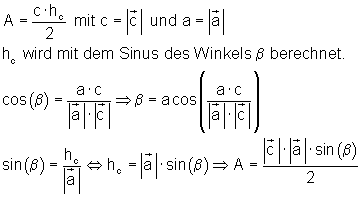
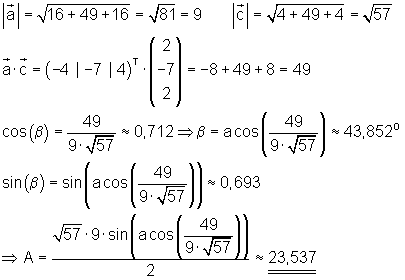
Die Probe bestätigt die erste Rechnung.
Zusammenfassung der Vektorregeln
Addition und Subtraktion von Vektoren
Multiplikation eines Vektors mit einem Skalar
Das Skalarprodukt
Das vektorielle Produkt
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Vektorrechnung.