In diesem Beitrag definiere ich zuerst das skalare Produkt. Dann erkläre die Rechengesetze dazu. Danach stelle ich Beispiele und Zeichnungen dazu zur Verfügung. Zuletzt definiere ich den euklidischer Vektorraum.
Definition: das skalare Produkt
Es wird auch Skalarprodukt genannt. Die Definition der Arbeit im physikalischen Sinne ist eine Verknüpfung zwischen zwei Vektoren, deren Ergebnis eine reelle Zahl ist.
![]()
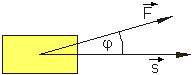
Das skalare Produkt \overrightarrow a \cdot \overrightarrow b zweier Vektoren wird berechnet, indem man das Produkt der Beträge dieser Vektoren mit dem Kosinus des von den Vektoren eingeschlossenen Winkels multipliziert:
\overrightarrow a \cdot \overrightarrow b = | \overrightarrow a | \cdot | \overrightarrow b | \cdot cos(\overrightarrow a, \overrightarrow b)
Rechenregel für das skalare Produkt:
Ein Skalarprodukt zweier Vektoren wird gleich Null, wenn mindestens einer der beiden Vektoren der Nullvektor ist oder wenn beide Vektoren senkrecht aufeinander stehen.
\overrightarrow a \cdot \overrightarrow b = 0 , wenn \overrightarrow a = 0 oder \overrightarrow b = 0 oder \overrightarrow a \perp \overrightarrow b . \\
Denn aus \overrightarrow a \perp \overrightarrow b folgt cos(\overrightarrow a , \overrightarrow b) = 0 . \\
D. h. \measuredangle (\overrightarrow a , \overrightarrow b) = 90° oder \measuredangle (\overrightarrow a , \overrightarrow b) = 270° .
Für die skalare Multiplikation zweier gleicher Vektoren folgt:
![]()
Mit Hilfe des Skalarprodukts kann der Betrag eines Vektors dargestellt werden.
![]()
Rechengesetze für skalare Produkte
Kommunikativgesetz, Assoziativgesetzt und Distributivgesetz:
Wenn du diese drei Gesetze noch einmal nachlesen willst, schaue hier.
Beispiel 1 zum skalaren Produkt:

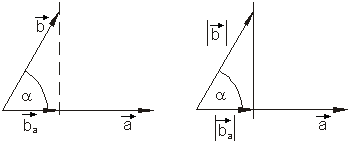
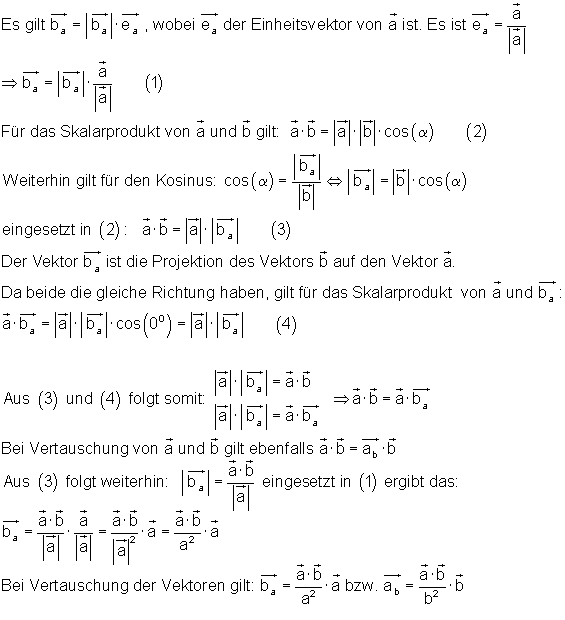
Zusammenfassend lässt sich sagen:
Der Wert des skalaren Produktes zweier Vektoren ändert sich nicht, wenn man einen der Vektoren durch seine Komponente längs des anderen ersetzt.
![]()
Da die Division zweier Vektoren nicht definiert ist, kann folgende Beziehung manchmal hilfreich sein:
![]()
Beispiel 2:

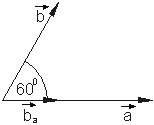
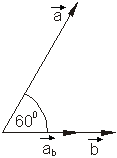
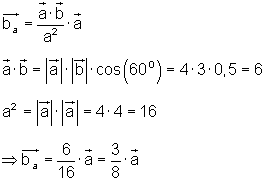
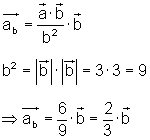
Beispiel 3:
Der Kosinussatz der ebenen Trigonometrie soll hergeleitet werden.
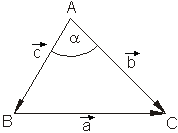
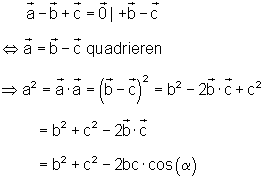
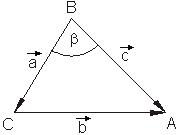
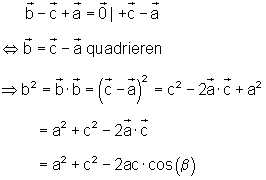
Besonderheit für ein rechtwinkliges Dreieck:
Da das Skalarprodukt zweier rechtwinklig aufeinanderstehender Vektoren Null ist, erhält man für obiges Beispiel den Satz des Pythagoras.
![]()
Beispiel 4:
Beweisen Sie, dass die Seitenhalbierende der Basis eines gleichschenkligen Dreiecks senkrecht auf dieser steht!
![]()
![]()
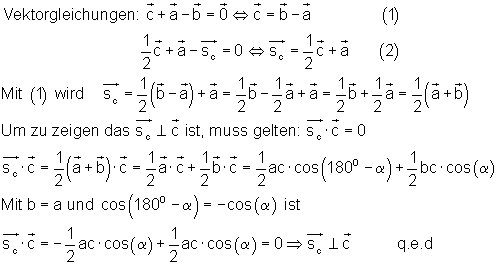
Definition Euklidischer Vektorraum
Gelten zusätzlich zur algebraischen Struktur eines reellen Vektorraums, wie nachfolgend aufgelistet, folgende Gesetze,


dann spricht man von einem euklidischen Vektorraum.
Bemerkungen zum Skalarprodukt:
Zu einem Vektor gibt es bezüglich der Skalarmultiplikation kein inverses Element. Das bedeutet, man kann durch einen Vektor nicht dividieren.
Bezüglich der Skalarmultiplikation von Vektoren gibt es kein neutrales Element, denn das Ergebnis ist eine reelle Zahl und kein Vektor.
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Vektorrechnung.

