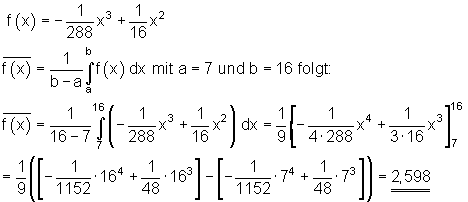Bis jetzt haben wir mit Hilfe der Integralrechnung Flächen zwischen einem Graphen und der x-Achse und Flächen zwischen Funktionsgraphen berechnet. In diesem Beitrag zeige ich zuerst ein Beispiel aus der Praxis. Wir können mit Integralen zum Beispiel die mittlere Flughöhe eines Fussballs im Bereich zwischen 7 m und 16 m nach dem Abschuss berechnen. Danach erkläre ich, wie man das Integral als Mittelwert von f(x) im Intervall [a; b] berechnet. Anschließend versuche ich den Ansatz über das bestimmte Integral. Zuletzt demonstriere ich die Berechnung der Beispielaufgabe.
Beispiel: Flughöhe eines Fussballs
Schauen wir uns dazu folgendes Beispiel an: Der Graph der Funktion f(x) ist näherungsweise die Flugkurve des Balls bei einem Freistoß in einem Fußballspiel. Hier die Formel dazu:
f(x) = -\frac{1}{288}x^3 + \frac{1}{6}x^2
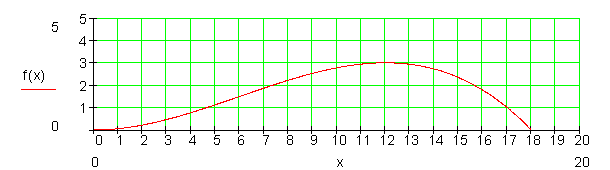
Zuerst legen wir für diesen Bereich eine Wertetabelle an:

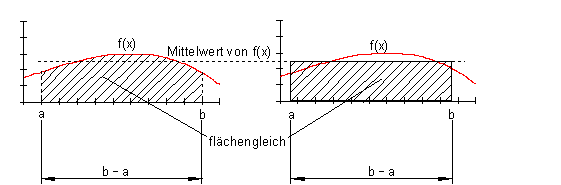
Das Integral als Mittelwert von f(x) im Intervall [a; b]
Der Ball hätte somit im Intervall [ 7 ; 16 ] eine mittlere Flughöhe von 2,512 m.
Würde man in gröberen oder feineren Schritten vorgehen, so bekäme man für den jeweiligen Mittelwert andere Ergebnisse.
Bei den x-Werten 7; 10; 13; 16 käme für den Mittelwert 2,34 m heraus.
Bei den x-Werten 7; 7,5; 8; 8,5; ….. käme für den Mittelwert 2,555 m heraus.
Offenbar scheint es so zu sein, dass je kleiner wir die x-Schritte wählen, desto genauer erhalten wir den Mittelwert.
Den Ansatz über das bestimmte Integral versuchen:


Beispielaufgabe zum Integral als Mittelwert:
Der Ball hätte also im Intervall [ 7 ; 16 ] eine mittlere Flughöhe von 2,598 m.
Das bestimmte Integral wird somit zu einer kontinuierlichen Verallgemeinerung des Begriffs der Summe. Das heißt, je kleiner man die x-Schritte macht, desto mehr nähert man sich an den Mittelwert der Funktion heran. Die Anzahl der Summanden wird dabei immer größer.
Hier eine Übersicht über alle Beiträge zur Integralrechnung, darin auch Links zu weiteren Aufgaben.