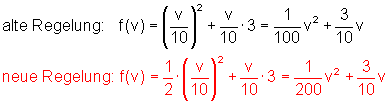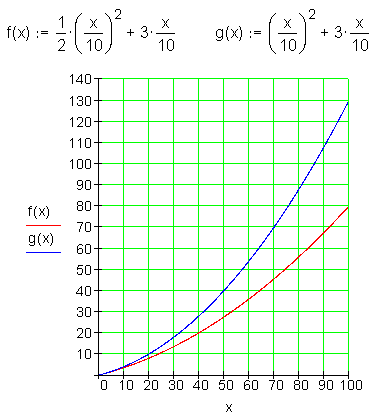Nachdem wir uns gründlich mit linearen Funktionen beschäftigt haben, führe ich in diesem Beitrag in quadratische Funktionen ein. Bevor es in die Theorie geht, stelle ich als erstes ein praktische Beispiel vor. Für dieses zeige ich anschließend die Funktionsgleichung, die Wertetabelle und den Graphen. Dabei wird deutlich, dass es sich um eine quadratische Funktion handelt. Der hierzu gehörende Graph wird Parbel genannt. Danach definiere ich die Begriffe Scheitelpunkt und Formfaktor und erkläre, wie der Formfaktor die Parabel verschiebt. Außerdem stelle ich einen interaktiven Parabelplotter und Parabelanalysator zur Verfügung. Zuletzt erkläre ich die Scheitelpunktbestimmung durch quadratische Ergänzung.
Quadratische Funktion Beispiel:
Der Anhalteweg eines bremsenden Autos auf trockener asphaltierter Straße setzt sich aus dem Reaktionsweg und dem Bremsweg zusammen.
Im folgenden die Faustregeln für den Reaktionsweg r und der Bremsweg b in Meter in Abhängigkeit von der Geschwindigkeit v in km/h .
Achtung: Mitteilung der Rheinischen Post vom 3.3.04
Ab 1. Juni 2004 berechnet man den Anhalteweg auf einer trockenen asphaltierten Straße mit einem anderen Bremsweg.

Bemerkung zu den Einheiten der Faustformel:
Der Brems- bzw. Reaktionsweg kommt in Meter (m) heraus, wenn die Geschwindigkeit in Kilometer pro Stunde (km/h) eingesetzt wird.
a) Bestimmen Sie für beide Fälle die Funktionsgleichung s = f(v), mit der für jede gefahrene Geschwindigkeit der Anhalteweg berechnet werden kann.
b) Stellen Sie für beide Fälle in einer Wertetabelle für folgende gefahrene Geschwindigkeiten v = 0, 10, 20, 30, … 100 km/h die jeweiligen Anhaltewege s zusammen.
c) Zeichnen Sie beide Graphen in ein Koordinatensystem.
d) Kommentieren Sie das Gesamtergebnis.
Problemlösung:
a) Die Funktionsgleichung
b) Die Wertetabelle
c) Die Graphen
Die x-Achse stellt die jeweils gefahrene Geschwindigkeit in km/h da.
Die y-Achse stellt den jeweiligen Anhalteweg in m da.
d) Der Kommentar
Nach der neuen Verordnung wird der Unterschied mit zunehmender Geschwindigkeit immer größer. Bei 50 km/h beträgt der neue Anhalteweg 27,5 m, das sind etwa 69% des alten Weges von 40 m. Bei 100 km/h beträgt der neue Anhalteweg jedoch nur noch 80 m, das sind etwa 61% des alten Weges von 130 m. Die Verringerung des Bremsweges ist wegen der besseren Bremsen (ABS) sinnvoll.
Bei genauer Betrachtung der Funktionsgleichungen und der Graphen stellen wir fest, das es sich weder um lineare Funktionen, noch um Geraden handelt.
Die Funktionsgleichungen haben die Form:
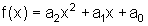
Da die Variable x hier in der 2. Potenz auftritt, nennt man solche Funktionen quadratische Funktion oder auch ganzrationale Funktionen 2. Grades.
Die Graphen hierzu werden Parabeln genannt.
Hierzu ein paar Aufgaben 1 bis 10
Arbeitsauftrag:
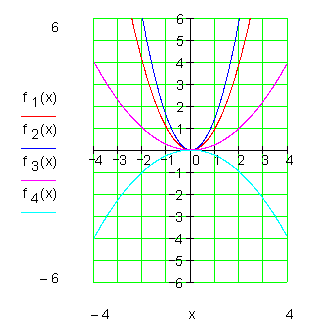
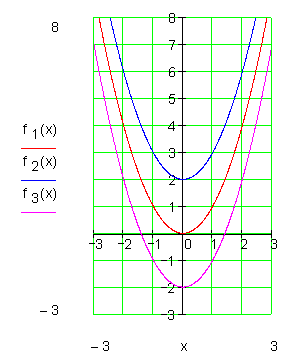
Die Funktionsgleichungen der abgebildeten Parabeln unterscheiden sich nur durch den Koeffizienten a2 von x2.
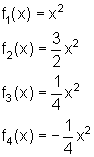
Definition Formfaktor
Dieser Koeffizient a2 ist für die Form der Parabel verantwortlich und heißt demnach Formfaktor.
Definition Scheitelpunkt
Der Scheitelpunkt S hat dieKoordinaten S ( 0 | 0 ).
Wie beeinflusst der Formfaktor die Gestalt der Parabel?

Parabelplotter: Interaktiv: Gib Werte für die einzelnen Teile des Terms ein, wähle Zoom, Gitterabstand und Zeichenfläche. Nachdem du auf ‚Zeichnen‘ geklickt haben, kannst du die Parabal bewundern.
Arbeitsauftrag:

Verschiebung der Normalparabel
Es handelt sich dabei um eine verschobene Normalparabel, deren Scheitelpunkt S um a0 Einheiten verschoben wurde.
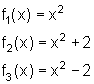
Die Verschiebung erfolgt längs der Ordinatenachse, wobei die Richtung der Verschiebung durch das Vorzeichen von a0 bestimmt wird.
Der Scheitelpunkt S hat dieKoordinaten S ( 0 | a0 ).
Parabelplotter: Interaktiv: Auch hierfür kannst du dir die Parabel zeichnen lassen.
Wenn eine Parabel symmetrisch zur y-Achse ist, können wir mit dem Scheitelpunkt S und einem der Schnittpunkte auf der x-Achse die Funktion aufstellen. Dazu kannst du dir dieses 📽️Video Quadratisch Funktion symmetrisch erstellen aus 2 Punkten ansehen.
Arbeitsauftrag:

Es handelt sich um eine verschobene Normalparabel, deren Scheitelpunkt S um u Einheiten auf der x -Achse verschoben wurde. Der Scheitelpunkt S hat die Koordinaten S ( -u | 0 )

Arbeitsauftrag:

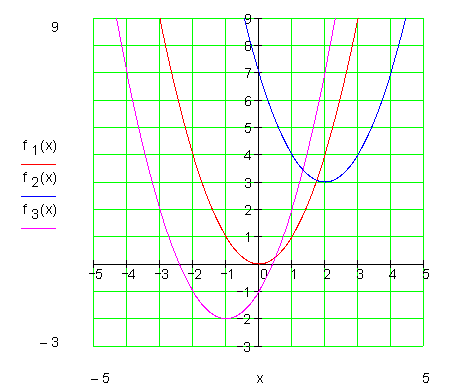
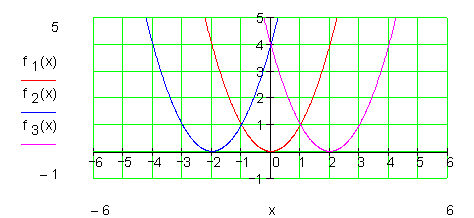
Der Graph von f2 (x) ist wieder eine Normalparabel, deren Scheitelpunkt S um zwei Einheiten nach rechts und um drei Einheiten nach oben verschoben ist.
Der Graph von f3 (x) ist ebenfalls eine Normalparabel, deren Scheitelpunkt S um eine Einheit nach links und um zwei Einheiten nach unten verschoben ist.
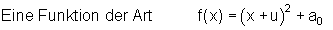
nennt man Scheitelpunktform der quadratischen Funktion.
Der Graph der Funktion ist eine Normalparabel, die um den Wert u in Richtung der Abszissenachse und um a0 in Richtung der Ordinatenachse verschoben ist.
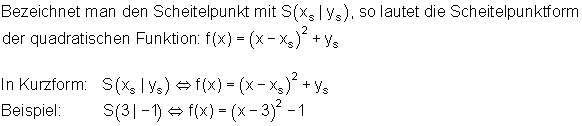
Bisher haben wir nur die Normalparabel verschoben.
Die gleichen Verschiebungen lassen sich auch mit einer beliebigen Parabel durchführen.
Dabei ist dann der Formfaktor a2 zu berücksichtigen.

Scheitelpunktbestimmung durch quadratische Ergänzung
Wir wissen bereits das gilt:![]()
Durch eine Termumformung der allgemeinen Funktionsgleichung in die Scheitelpunktform lässt sich der Scheitelpunkt einer Parabel ermitteln.
1. Beispiel:
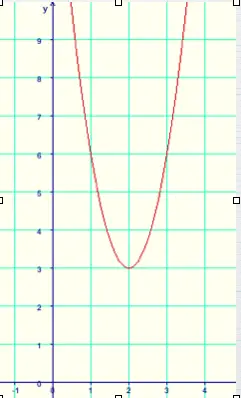
Wir berechnen den Scheitelpunkt der Funktion f(x) = 3x^2 - 12x + 15 . Sie hat keinen Schnittpunkt mit der x-Achse, deshalb können wir den Scheitelpunkt nicht über die Nullstellen berechnen.
1. Schritt: Wir klammern den Faktor von x2 aus:
\Rightarrow f(x) = 3 \cdot [x^2 - 4x + 5]
2. Schritt: Quadratische Ergänzung: p ist der Faktor, mit dem x multipliziert wird, hier -4. Also ist (\frac{p}{2})^2 = 2^2 . Das addieren und subtrahieren wir und erhalten:
\Leftrightarrow f(x) = 3 \cdot [ x^2 - 4x \color{red}{ +2^2 - 2^2} \color{black}{ + 5}]
Dabei entspricht x^2 - 4x + 2^2 der 2. binomischen Formel. Deshalb könner wir es umwandeln in (x - 2)^2 . Dadurch erhalten wir:
\Leftrightarrow f(x) = 3 \cdot [ (x - 2)^2 - 2^2 + 5] .
\Leftrightarrow f(x) = 3 \cdot [ (x - 2)^2 + 1]
Zuletzt lösen wir die eckige Klammer auf, indem wir die 3 mit den beiden Summanden multiplizieren
\Leftrightarrow f(x) = 3 (x - 2)^2 +3
Das ist die Scheitelform der quadratischen Funktion. Daraus können wir den y-Wert +3 und den x-Wert -2 mal -1 = 2 direkt ablesen. Also ist S (2 | 3).
Dazu kannst du dir dieses 📽️Video Quadratische Ergänzung Scheitelpunkt bestimmen ansehen
2. Beispiel:
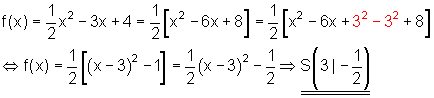
3. Beispiel:
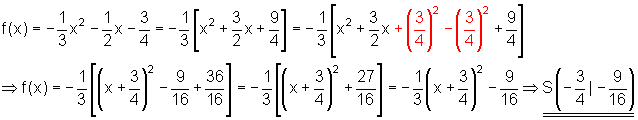
Parabelanalysator Interaktiv: Gib die Koeffizienten ein, klick danach auf ‚Zeichnen‘ und ‚Berechnen‘.
Hierzu jetzt die Trainingsaufgaben 11 bis 20.
Hier findest du die Aufgaben Grundladen Quadratische Funktionen I.
Dazu hier eine Übersicht über weitere Beiträge zu Quadratischen Funktionen, darin auch Links zu weiteren Aufgaben.
Im nächsten Beitrag beschäftigen wir uns näher mit Achsenschnittpunkten, der p-q-formel und- Lnearfaktoren.