In diesem Beitrag erkläre ich zuerst, was eine Kurvendiskussion ist und was man dabei beachten sollte. Danach gebe ich eine bewährte Anleitung für die Kurvendiskussion. Anschließend erkläre ich dies anhand eines Beispiels. Dabei zeige ich auch die Berechnung mit dem Casio fx-CG20 und Casio fx-CG50. Schließlich stelle ich Aufgaben zur Verfügung.
Was ist eine Kurvendiskussion?
Wenn man den Graph einer Funktion zeichnen will, muss man ihre wichtigsten Eigenschaften untersuchen. Mit anderen Worten, seine markanten Punkte und seinen Verlauf im Definitionsbereich bestimmen. Das ist Kurvendiskussion.
Damit man keine wichtigen Eigenheiten der Funktion übersieht, sollte man systematisch vorgehen. Das heißt immer die gleiche Reihenfolge der Berechnungen einhalten.
Anleitung für die Kurvendiskussion:
1. Definitionsbereich:
Zuerst bestimmt man den Definitionsbereich der Funktion. Denn nur innerhalb dieses Bereiches ist es sinnvoll, Untersuchungen über die Eigenschaften der Funktion anzustellen.
2. Symmetrien:
siehe: Symmetrie und Verlauf ganzrationaler Funktionen.
Dazu kannst du dir das 📽️ Video Symmetrie und Verlauf ganzrationaler Funktionen ansehen.
Dann stellt man fest, ob die Funktion achsen- oder punktsymmetrisch ist.
![]()
Speziell bei ganzrationalen Funktionen gilt:
Eine ganzrationale Funktion ist genau dann achsensymmetrisch, wenn ihr Term nur Summanden mit geraden Exponenten enthält.
Eine ganzrationale Funktion ist genau dann punktsymmetrisch, wenn ihr Term nur Summanden mit ungeraden Exponenten enthält.
3. Extrempunkte:
siehe auch: Extrempunkte berechnen.
Außerdem kannst du dir die beiden Videos 📽Extrempunkte in der Differentialrechnug und 📽 Extrempunkt hinreichende Bedingung ansehen.
Als nächstes bestimmt man die relativen Extrema. Mit anderen Worten die Hoch- bzw. Tiefpunkte.
Das sind auch die Punkte mit waagerechter Tangente.
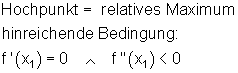

4. Wendepunkte:
Siehe auch: Wendepunkt, Sattelpunkt und Wendetangente.
Dazu kannst du dir die Videos 📽Wendepunkte berechnen und 📽️Sattelpunkt berechnen ansehen.
Danach bestimmt man die Wendepunkte bzw. die Sattelpunkte.
![]()
Sattelpunkt ist ein Wendepunkt mit waagerechter Tangente.
5. Achsenschnittpunkte:
Siehe auch: Achsenschnittpunkte und Nullstellenberechnung.
Dazu kannst du dir das 📽️ Video Faktorierungsverfahren ansehen.
Wenn die Hochpunkte < 0, dann gibt es keine Nullstellen. Wenn die Tiefpunkte > 0 ebenfalls nicht.
Nullstellen sind oft Teiler des absoluten Gliedes, mit anderen Worten die Zahl, die hinten alleine steht. Wenn einen Nullstelle bekannt ist, können die anderen mithilfe der Polynomdivision oder mit dem Hornerschema berechnet werden.
Außerdem kannst du dir die Videos 📽️Polynomdivision, 📽️Horner-Schema und 📽️Hornerschema ersetzt Polynomdivision ansehen.
Wird der x-Wert Null ( x = 0 ) in die Funktionsgleichung von f(x) eingesetzt, erhält man den Schnittpunkt mit der y-Achse.
Die Schnittpunkt(e) mit der x-Achse erhält man durch Nullsetzen des Funktionsterms von f(x).

6. Den Graphen zeichnen:
Mit allen bisher gesammelten Informationen lässt sich in den meisten Fällen nun der Graph zeichnen.
Dazu wird zunächst eine Wertetabelle angelegt.
Dabei zeigt es sich, welche Werte noch zu berechnen sind.
Diese kann man entweder mit dem Taschenrechner bestimmen, oder für ganzzahlige x-Werte mit dem HORNER-Schema.
Außerdem kannst du dir das 📽️Video Horner-Schema ansehen.
7. Krümmungsverhalten und Monotonie:
Siehe auch: Monotonieeigenschaften.

Das heißt:
An den Wendestellen ändert sich das Krümmungsverhalten eines Graphen. Das Monotonieverhalten dagegen ändert sich an den Extremstellen.
8. Randpunkte des Definitionsbereiches:
Zueletzt untersuchen wir die Funktion in den Randpunkten des Definitionsbereichs. Wenn der Definitionsbereich nicht beschränkt ist, dann muss man die beiden Grenzwerte bestimmen.
![]()
Anders ausgedrückt: Man betrachtet den Verlauf der Funktionswerte für große x-Werte in sowohl positiver als auch negativer Richtung und fragt sich, wohin die Funktionswerte gehen.
Beispiel einer ausführlichen Kurvendiskussion
1. Definitionsbereich:
![]()
Die Funktion ist für alle reellen Zahlen definiert. Normalerweise gilt das immer für ganzrationale Funktionen. Es sei denn, man möchte die Definitionsmenge einschränken.
2. Symmetrien:
Weil alle Exponenten gerade sind, liegt hier eine Achsensymmetrie vor.
![]()
Der Vorteil besteht hierbei darin, dass Funktionswerte nur für positive x-Werte berechnet werden müssen. Für die entsprechend negativen x-Werte sind sie folglich identisch.
3. Extrema:
Man bildet zuerst die ersten beiden Ableitungen der Funktion f(x).
Wenn man die 1. Ableitung gleich Null setzt, liefert sie die Stellen mit waagerechter Tangente.
Danach setzt man diese Werte in die 2. Ableitung ein. Dadurch erhält man eine Aussage über die Art des vorliegenden Extremums.
(Relatives Maximum oder relatives Minimum, bzw. kein Extrempunkt).
Wenn man die Werte der Extremstellen xi in die Funktionsgleichung einsetzt, ergeben sich die Extremwerte. Damit sind die Koordinaten der Extrempunkte bekannt.
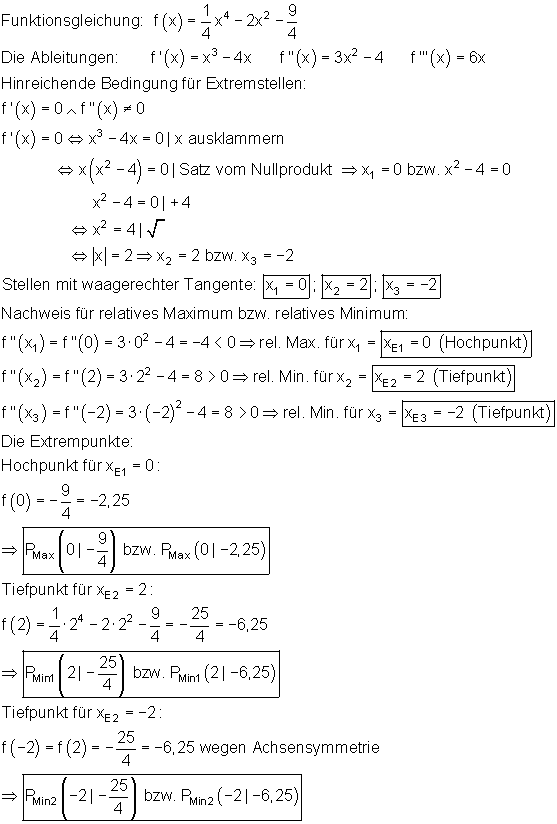
Die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 habe ich unten erklärt.
4. Wendepunkte:
Zusätzlich zu den ersten beiden Ableitungen von f(x) bildet man danach die dritte.
Die Nullstellen der zweiten Ableitung sind mögliche Wendestellen.
Zur Überprüfung ob ein Wendepunkt vorliegt, setzt man die errechneten Nullstellen der zweiten Ableitung in die dritte Ableitung ein.
Wenn das Ergebnis ungleich Null ist, bezeichnet der entsprechende x-Wert eine Wendestelle. Den dazugehörigen Funktionswert erhält man dann durch Einsetzen der x-Werte in den Term der Funktionsgleichung f(x).
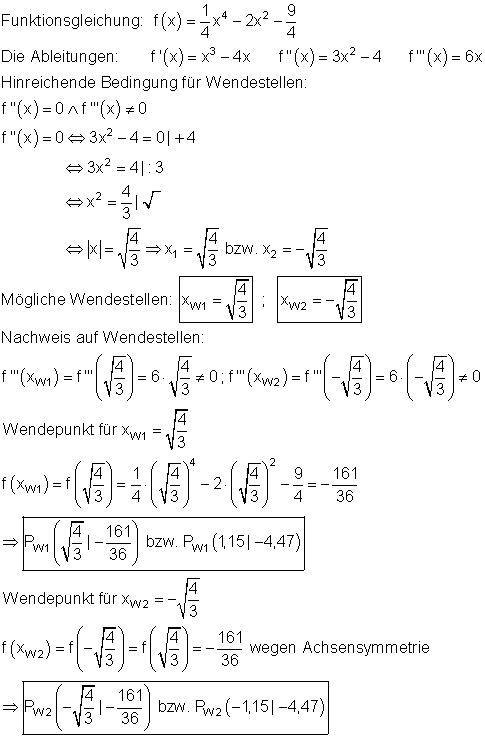
Die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 habe ich unten erklärt.
5. Achsenschnittpunkte:
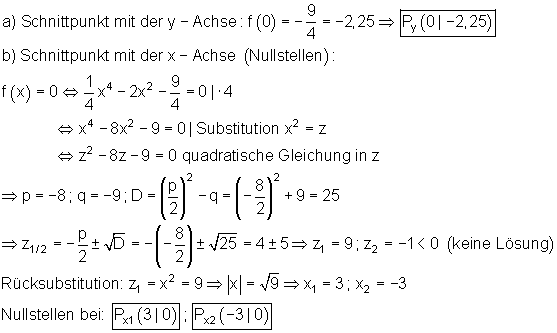
Die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 habe ich unten erklärt.
6. Wertetabelle und Graph:

Die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 habe ich unten erklärt.
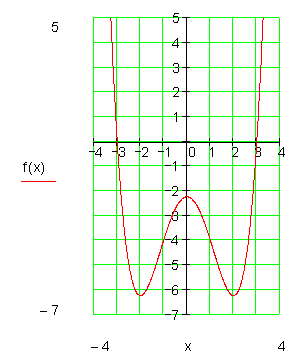
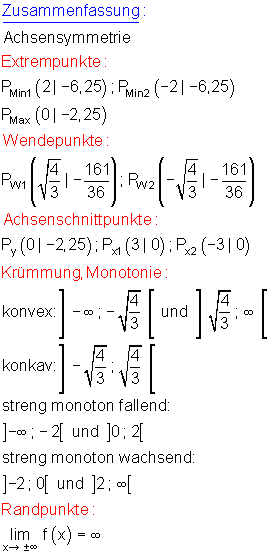
7. Krümmungsverhalten und Monotonie:
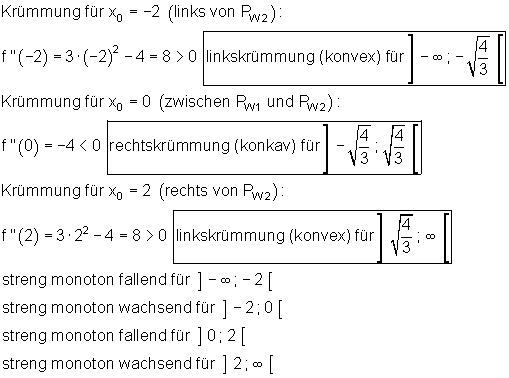
8. Randpunkte des Definitionsbereiches:
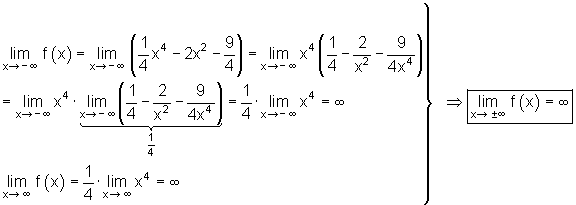
Interaktiv: Kurvendiskussion:
Gib einen ganzrationalen Term ein, das Javascript erstellt dann die Kurvendiskussion.
Interaktiv: Nullstellenfinder:
Gib einen Term ein, das Javascript berechnet die Nullstellen von Polynomen bis 9. Grades und zeichnet den Funktionsgraphen.
Berechnungen mit dem GTR Casio fx-CG20 und Casio fx-CG50
Dort findest du auch eine Anleitung, wie man den Casio fx-CG20 auf den Casio fx-CG50 updaten kann.
1. Berechnen Sie die Extrempunkte von
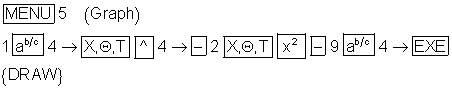
x: [ -4 ; 4 ] und y: [ -7 ; 5 ] eingestellt.
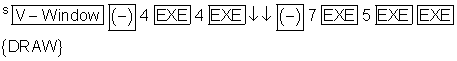
Extremwerte:
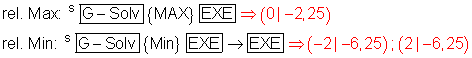
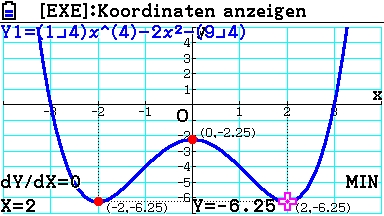
Mit [EXIT] gelangt man dann zurück in den Grafikeditor.
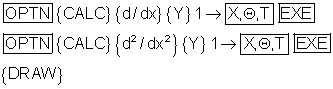
Die Wendestelle liegt dort, wo die zweite Ableitung Null ist.

Die Wendestellen liegen folglich bei xw1 = -1,1547.. und xw2 = 1,1547..
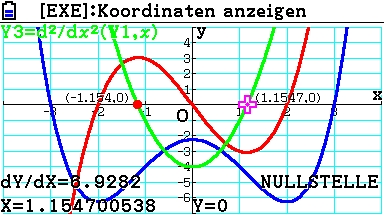
Der zugehörige Wendepunkt hat die Koordinaten:

Pw1 ( -1,1547.. | -4,472..) ; Pw2 ( 1,1547.. | -4,472..)
Diese Werte sind ungenau, aber mit SolveN wird die Berechnung präziser.
Die Nullstellen von f“(x) = 3x2 – 4 liefern danach die Wendestellen.
Die Nullstellen von f“(x) also xw1 und xw2 berechnet man mit SolveN und speichert sie dann in Liste 3 ab.
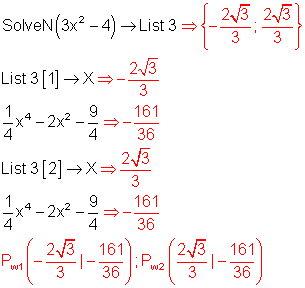
Eingabeprozedur:

3. Berechne die Achsenschnittpunkte von
Mit S[Sketch] {Cls} kann man danach den Graph neu zeichnen. Der Schnittpunkt mit der y-Achse ist deshalb:
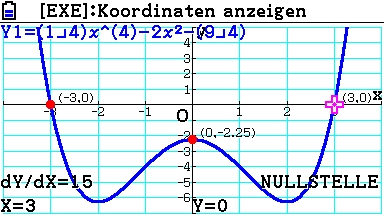
4. Wertetabelle erstellen für
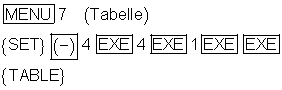
Wertetabelle (gerundet auf 2 Stellen):
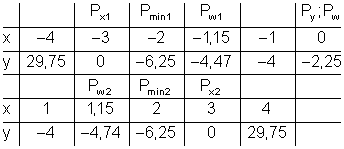
Dazu findest du weitere Beispiele in der Kategorie GTR.
Außerdem in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.
Eine Einführung in den Casio fx-CG20 findest du hier.
Hier findest du Aufgaben Differenzialrechnung XI.
Hier Aufgaben zur Kurvendiskussion ganzrationaler Funktionen.
In den nächsten 5 Beiträgen stelle ich dann ausführliche Beispiele vor,

