Wenn du den Dreisatz verstehen und anwenden willst, bist du hier richtig. In diesem Beitrag wird der Dreisatz einfach erklärt.
Dazu sehen wir uns als erstes die drei Schritte des Dreisatzes anhand eines einfach Beispiels an. Diese drei Schritte – oder auch Sätze – geben dem Dreisatz seinen Namen.
Danach erkläre ich dir anhand einfacher Beispiele, welche Arten des Dreisatzes es gibt und zeige dir auch, wie du sie erkennst:
- Einfacher Dreisatz proportional
- Einfacher Dreisatz antiproportional
- Tabellarische Darstellung des einfachen Dreisatzes
- Zweifach verschachtelter Dreisatz proportional-proportional
- Zweifach verschachtelter Dreisatz antiproportional-proportional
- Dreifach verschachtelter Dreisatz proportional-antiproportional-antiproportional
Keine Sorge! Dies ist einfacher als es jetzt klingt!
Am Ende des Beitrags findest du einen Link zu Übungsaufgaben und ausführlichen Lösungen.
Beispiel einfacher Dreisatz:
Ein Gartenbauer verlegt in 8 Stunden 200 m² Rollrasen. Wieviel Rollrasen würde er bei gleicher Leistung in 13 Stunden verlegen?
Tipp zum Lösen der Dreisatzaufgaben:
Wenn du eine Aufgabe lösen willst, überlege immer, wonach wir suchen!
Hier ist die gesuchte Größe die Anzahl der Quadratmeter Rollrasen.
In drei einfachen Schritten – die Dreisatzformel:
1. Satz: Bekanntes Verhältnis
2. Satz: Schluss auf die Einheit
3. Satz: Schluss auf die gesuchte Mehrheit
1. Satz: Bekanntes Verhältnis: In 8 Stunden 200 m²
2. Satz: Schluss auf die Einheit: In 1 Stunde den 8. Teil
3. Satz: Schluss auf die gesuchte Mehrheit: In 13 Stunden 13 mal soviel.
In 8 Stunden 200m²
In 13 Stunden ? m²
In 8 Stunden 200m²
In 1 Stunde den 8.Teil davon, in 13 Stunden 13 mal so viel
Daraus entsteht zur Rechnung ein Bruch, bei dem der Ausgangswert (hier 200 m²) im Zähler steht. Der Teil steht im Nenner (hier 8), wie viel mal steht im Zähler (hier 13):
\frac{200m^2 \cdot \color{red}{13}}{\color{blue}{8}} = 325m^2
In diesem Fall braucht der Gartenbauer mehr Zeit, je mehr Rasen er verlegt. Deshalb spricht man hier von einer proportionalen Zuordnung. Das erkläre ich gleich genauer.
Lösung:
In 13 Stunden würde der Gartenabeiter 325 m² Rollrasen verlegen.
💡 Grundsatz:
Bei Dreisatzrechnungen sind die Zuordnungen entweder proportional oder antiproportional.
1. Einfacher Dreisatz proportional
Wann ist der Dreisatz proportional?
Wenn zwei Größen im gleichen Verhältnis zu- oder abnehmen, spricht man von einer proportionalen Zuordnung.
Beispiele:
- Je mehr Kilometer ein Auto fährt, desto mehr Benzin benötigt es.
- Je weniger am Tag gearbeitet wird, desto weniger Lohn erhält man.
Anders ausgedrückt:
- Zum Doppelten der einen Größe gehört das Doppelte der anderen Größe.
- Zur Hälfte der einen Größe gehört die Hälfte der anderen Größe.
Wenn sich zwei Größen im gleichen Maße verändern, dann muss man sie auch genauso berechnen.
Falls man also die eine Größe mit einer Zahl multipliziert, muss man auch die andere Größe mit derselben Zahl multiplizieren.
Wenn man die eine dividiert, muss man die andere auch mit der gleichen Zahl dividieren.
Sobald man das verstanden hat, ist der Dreisatz einfach.
Beispiel:
- doppelte Menge → doppelte Kosten
- halbe Menge → halbe Kosten
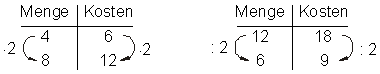
entsprechend gilt auch:
- vierfache Menge → vierfache Kosten
- ein Viertel der Menge → ein Viertel der Kosten
Beispiel:
Ein Pkw verbraucht auf 100 km 9,6 Liter Benzin. Mit einer Tankfüllung kommt er 540 km weit.
Wie viel Liter fasst der Tank? Das Ergebnis ist auf ganze Liter aufzurunden.
100km 9,6 Liter
540km ? Liter
100km 9,6 Liter
1km der 100. Teil
540km 540 mal so viel
\frac{9,6l \cdot \color{red}{540}}{\color{blue}{100}} = 51,84l \approx 52l
Es handelt sich um einen proportionalen Zusammenhang.
Je mehr Kilometer das Auto fährt, desto mehr Liter Benzin benötigt es.
In Kurzform:
Je mehr Kilometer, desto mehr Liter ⇒ proportional
Antwort: Der Tank fasst 52 Liter.
Bemerkung: Zwischenergebnisse sind nicht nötig, die Zahl vor dem Wort „mal” steht in der Rechnung auf dem Bruchstrich, die Zahl vor dem Wort „Teil” steht im Nenner. Das gilt für alle Aufgaben.
Dazu kannst du dir dieses 
2. Einfacher Dreisatz antiproportional
Wann ist der Dreisatz antiproportional?
Wenn zwei Größen im umgekehrten Verhältnis zu- oder abnehmen, spricht man von einer antiproportionalen Zuordnung.
Beispiele:
- Je mehr Arbeiter für eine bestimmte Arbeit zur Verfügung stehen, desto weniger Zeit ist erforderlich.
- Je langsamer ich fahre, desto mehr Zeit benötige ich für eine bestimmte Strecke.
Anders ausgedrückt:
- Zum Doppelten der einen Größe gehört die Hälfte der anderen Größe.
- Zur Hälfte der einen Größe gehört das Doppelte der anderen Größe.
Deshalb gilt hier das Umgekehrte als beim proportionalen Dreisatz:
Wenn zwei Größen im umgekehrten Verhältnis zu- oder abnehmen, muss man sie auch anders berechnen!
Falls man also die eine Größe mit einer Zahl multipliziert, muss man die andere Größe durch dieselbe Zahl dividieren.
Wenn man die eine dividiert, muss man die andere mit der gleichen Zahl multiplizieren.
Beispiel:
- doppelte Geschwindigkeit → halbe Zeit
- halbe Geschwindigkeit → doppelte Zeit
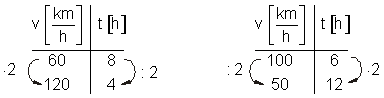
entsprechend gilt auch:
- vierfache Geschwindigkeit → ein Viertel der Zeit
- ein Viertel der Geschwindigkeit → vierfache Zeit
Dazu kannst du dir dieses 
3. Tabellarische Darstellung des einfachen Dreisatzes
Den einfachen Dreisatz kann man auch in verkürzter Form tabellarisch darstellen.
Beispiel 1:
5 kg Bananen kosten 9 Euro.
Wie teuer sind 7 kg Bananen derselben Sorte?
proportional

7 kg Bananen kosten 12,60 Euro.
Beispiel 2:
Bei einer mittleren Geschwindigkeit von 60km/h dauert die Fahrt von Duisburg nach Frankfurt 5 Stunden.
Wie lange dauert die Fahrt bei einer mittleren Geschwindigkeit von 80km/h?
antiproportional

Bei einer mittleren Geschwindigkeit von 80 km/h dauert die Fahrt 3,75 Stunden.
Beispiel 3:
Nach einer großen Gartenparty brauchen 4 Helfer 3 Stunden für die Aufräumarbeiten. Wie lange dauert das Aufräumen mit 6 Helfern?
Überlegung: Die gesuchte Größe ist die Aufräumzeit in Stunden.
4 Helfer brauchen 3 Stunden
6 Helfer brauchen ? Stunden
4 Helfer brauchen 3 Stunden
1 Helfer braucht 4 mal so lange
6 Helfer brauchen den 6.Teil:
\frac{3h \cdot 4}{6} = 2h
Je mehr Helfer, desto weniger Stunden → antiproportional
1. Satz: Bekanntes Verhältnis: 4 Helfer brauchen 3 h2
2. Satz: Schluss auf die Einheit: 1 Helfer braucht 4 mal solange
3. Satz: Schluss auf die gesuchte Mehrheit: 6 Helfer brauchen 6 mal soviel
Antwort:
Mit 6 Helfern dauert das Aufräumen 2 Stunden.
Beispiel 4:
Drei Pflasterer benötigen für eine Hofeinfahrt 11,5 Stunden.
Wie lange brauchen 5 Pflasterer?
Dies ist ein Beispiel für einen antiproportionalen Zusammenhang. Je mehr Pflasterer arbeiten, desto schneller sind sie fertig, also desto weniger Stunden brauchen sie.
3 Pflasterer brauchen 11,5 Stunden
5 Pflasterer brauchen ? Stunden
3 Pflasterer brauchen 11,5 Stunden
1 Pflasterer braucht 3 mal so lange
5 Pflasterer brauchen den 5. Teil der Zeit
\frac{11,5h \cdot 3}{5} = 6,9h
Je mehr Pflasterer, desto weniger Stunden → antiproportional
Antwort:
5 Pflasterer brauchen 6,9 Stunden, also etwa 7 Stunden.
4. Zweifach verschachtelter Dreisatz proportional-proportional
Beispiel:
Ein 7m2 großes Kupferblech, 5mm dick und wiegt 313,6kg.
Wieviel wiegt ein 6mm dickes Kupferblech, das eine Fläche von 4m2 hat?
Es ist auf ganze Kilogramm zu runden.
In dieser Aufgabe haben wir die Größe des Blechs, seine Dicke und sein Gewicht. Also drei Dinge. Eines davon kennen wir nicht, zwei müssen wir berücksichtigen:
Je dicker und größer das Blech ist, desto schwerer ist es. Deshalb müssen wir zweimal rechnen.
Je mehr Millimeter, desto schwerer das Blech → proportional
Je mehr Quadratmeter, desto schwerer das Blech → proportional
7m² Blech · 5mm dick · 313,6kg
4m² Blech · 6mm dick · ? kg
7m² Blech · 5mm dick · 313,5kg
1m² Blech · 5mm dick · den 7. Teil
4m² Blech · 5mm dick · 4 mal so viel
4m² Blech · 5mm dick · den 5.Teil
4m² Blech · 6mm dick · 6 mal so viel
\frac{313,6kg \cdot \color{red}{4} \cdot \color{orange}{6}}{\color{blue}{7} \cdot \color{green}{5}} = 215,04kg \approx 215kg
Antwort:
Das Kupferblech wiegt etwa 215 kg.
💡 Tipp:
Wenn in einer Aufgabe drei Dinge erwähnt werden, musst du einen zweifach verschachtelten Dreisatz rechnen.
Hier kannst du dir eine ähnliche Aufgabe als 
5. Zweifach verschachtelter Dreisatz antiproportional-proportional
Beispiel:
Um eine Fläche von 720m² zu pflastern, brauchen 7 Maurer 160 Stunden.
Wie lange benötigen 5 Maurer für eine Fläche von 600m²?
Die Zeit ist in Stunden und Minuten anzugeben.
Zuerst wird über die Maurer, dann über die Fläche geschlossen.
7 Maurer · 720m² · 160h
5 Maurer · 600m² · ? h
7 Maurer · 720m² 160h
1 Maurer · 720m² · 7 mal so lange
5 Maurer · 720m² · den 5. Teil der Zeit
5 Maurer · 1m² · den 720. Teil der Zeit
5 Maurer · 600m² · 600 mal so lange
\frac{160h \cdot \color{red}{7} \cdot \color{orange}{600}}{\color{blue}{5} \cdot \color{green}{720}} = 186, \overline{6}h = 186 \frac{2}{3}h = 186h \, 40min
Antwort: 5 Maurer brauchen 186 Stunden und 40 Minuten.
Hier handelt es sich um eine Mischung aus einer proportionalen und einer antiproportionalen Beziehung:
- Je mehr Maurer pflastern, desto schneller sind sie fertig → antiproportional
- Je größer die Fläche ist, desto länger brauchen sie → proportional
In Kurzform:
Je mehr Maurer, desto weniger Stunden → antiproportional
Hier kannst du dir eine ähnliche Aufgabe als 

6. Dreifach verschachtelter Dreisatz proportional-antiproportional-antiproportional
Beispiel:
Zwölf Einschaler haben bei 9-stündiger Arbeitszeit in 7 Tagen 390m² Betonschalung hergestellt.
Wie viele Einschaler sind bei gleicher Leistung einzusetzen, wenn in insgesamt 21 Tagen 2340m² Betonschalung hergestellt werden müssen und die tägliche Arbeitszeit statt der üblichen 9 Stunden, nur noch 8 Stunden beträgt?
Hier sollst du die Anzahl der Einschaler berechnen.
Wir haben hier wieder eine Mischung aus proportionalen und antiproportionalen Zusammenhängen:
- Je größer die einzuschalende Fläche ist, desto mehr Einschaler werden benötigt und
- und je mehr Zeit zur Verfügung steht, desto weniger Einschaler braucht man
- je geringer die Arbeitszeit pro Tag ist, desto mehr Einschaler braucht man.
In Kurzform:
- Je mehr Quadratmeter, desto mehr Einschaler → proportional
- Und je mehr Tage, desto weniger Einschaler → antiproportional
- Je weniger Stunden, desto mehr Einschaler → antiproportional
💡 Tipp:
Wenn in einer Aufgabe vier Dinge erwähnt werden, musst du einen dreifach verschachtelten Dreisatz rechnen.
390m² · 7 Tage · 9 Stunden · 12 Einschaler
2340m² · 21 Tage · 8 Stunden · ?
390m² · 7T · 9h · 12E
1m² · 7T · 9h · den 390. Teil
2340m² · 7T · 9h · 2340 mal so viel
2340m² · 1T · 9h · 7 mal so viel
2340m² · 21T · 9h · den 21. Teil
2340m² · 21T · 1h · 9 mal so viel
2340m² · 21T · 8h · den 8. Teil
\frac{12E \cdot \color{red}{2340} \cdot \color{orange}{7} \cdot \color{gold}{9}}{\color{blue}{390} \cdot \color{green}{21} \cdot \color{aqua}{8}} = 27E
Antwort:
Man braucht 27 Einschaler.

