Durch Verknüpfungen von Mengen lassen sich andere Mengen bilden, die zu ihren Ausgangsmengen in bestimmten Beziehungen stehen. Dies ist in der Mathematik von Bedeutung, um Schreibweisen zu vereinfachen und das Erkennen von Strukturen zu erleichtern. Die wichtigsten Verknüpfungen sind Schnittmenge, Vereinigungsmenge, Restmenge und Produktmenge.
Definition Schnittmenge
Eine der häufigsten Verknüpfungen von Mengen ist die Schnittmenge. Das ist diejenige Menge, deren Elemente sowohl in der einen als auch in der anderen Ausgangsmenge enthalten sind
C = A \cap B = \{ x | x \in A \land x \in B \} Verknüpfungszeichen \cap
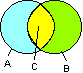
Die Menge C ist die Schnittmenge von A und B oder kurz ausgedrückt, C ist gleich A geschnitten B.
Die Schnittmengenbildung ist nicht auf zwei Mengen beschränkt.
S = \{ x | x \in A \land x \in B \land x \in C \land ... \} S = A \cap B \cap C \cap ...
Beispiel Schnittmenge:
Gegeben sind die Mengen A und B, wobei:
A = { x | 3 ≤ x ≤ 7}ℝ = [3; 7]
B = { x | -1 ≤ x ≤ 4}ℝ = [-1; 4[
![]()
![]()
Die Schnittmenge von A und B: A ∩ B Mit anderen Worten: A geschnitten B.
![]()
A ∩ B enthält alle Elemente, die in A und gleichzeitig in B liegen.
A ∩ B = [3; 4[
A ∩ B = { x | x ∈ A ∧ x ∈ B}
x ∈ A ∩ B heißt: x liegt in A und in B
Beispiel Schnittmenge
Gegeben sind die Mengen A und B mit A = {a ; b ; c ; d ; e ; f ; g} und B = {e ; f ; g ; h ; i ; j}
Ermitteln Sie die Schnittmenge!
C = A ∩ B = {e; f; g}
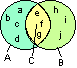
Die Elemente e, f und g sind sowohl in der Menge A als auch in der Menge B enthalten.
Beispiel Schnittmenge:
Die Schule bietet Kurse in Fotografie, Informatik und Digitaltechnik an, die die Schüler auf freiwilliger Basis besuchen können. Von der Klasse SF33S mit 20 Schülern wählen:
Neun Schüler den Fotokurs F 
Zwölf Schüler den Informatikkurs I und ![]()
Elf Schüler den Digitalkurs D ![]()
Drei Schüler belegen F und I, sind also in beiden AG’s 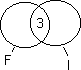
Fünf Schüler belegen F und D 
Sechs Schüler belegen I und D 
Zwei Schüler belegen alle drei AG’s also F, I und D 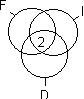
Wie viele Schüler besuchen nur einen Kurs?
Rechnung Schnittmenge:

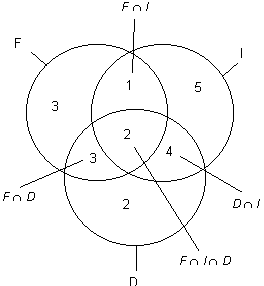
Über die gesamte Anzahl der Elemente in der Menge F, I und D lässt sich der verbleibende Rest in der Mengenschleife ermitteln. Damit belegen 10 Schüler nur einen Kurs.
Definition Teilmenge:
Die nächste Verknüpfung von Mengen ist die Teilmenge. Eine Menge A ist Teilmenge einer Menge B, wenn jedes Element von A auch Element von B ist.
A ⊂ B wenn gilt: alle Elemente von A sind auch Elemente von B.
Beispiel Teilmenge:
Die Klasse K besteht aus Jungen und Mädchen.
J ist die Menge der Jungen, M ist die Menge der Mädchen.
Deshalb gilt:
Die Menge der Jungen ist eine Teilmenge der Klasse.
Die Menge der Mädchen ist eine Teilmenge der Klasse.
J ⊂ K und M ⊂ K
Mit Hilfe der Schnittmenge kann man bestimmte Strukturen innerhalb der Mengenlehre erkennen.
Teilmenge und Schnittmenge
Wenn B eine Teilmenge von A ist, so ist die Schnittmenge von A und B gleich der Menge B.
B ⊂ A ⇔ A ∩ B = B.
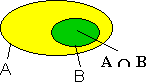
Diese kann man leicht aus dem Mengendiagramme erkennen.
Leere Schnittmenge
Die Schnittmenge disjunkter (elementfremder) Mengen ist leer.
Bildet man die Schnittmenge zweier elementfremder (disjunkter) Mengen, so findet sich kein Element, dass sowohl in der einen als auch in der anderen Menge enthalten ist. Diese Menge, die kein Element enthält, heißt leere Menge.
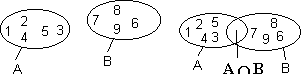
A ∩ B = { } = ∅
Das Kurzzeichen für die leere Menge wird mit dem Symbol Ø gekennzeichnet.
Schnittmenge und Kommutativgesetz
Für die Schnittmengenbildung gilt das Kommutativgesetz. Das heißt, man kann die beiden Mengen vertauschen.
![]()
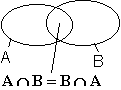
Auch diese kann man leicht aus dem Mengendiagramme erkennen.
Definition Vereinigungsmenge
Man kann Mengen auch verknüpfen, indem man sie vereinigt. Die Vereinigungsmenge ist diejenige Menge, deren Elemente entweder in der einen Menge oder in der anderen Menge oder in beiden enthalten sind.
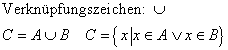
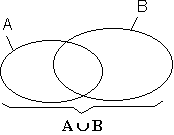
Die Menge C ist die Menge A vereinigt mit der Menge B.
Es können auch mehrere Mengen miteinander vereinigt werden:
![]()
Beispiel Vereinigungsmenge:
Vereinigungsmenge
![]()
![]()
![]()
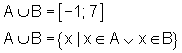
![]()
Beispiel Vereinigungsmenge:
Gegeben sind die Mengen A und B in beschreibender Form:
![]()
Die Vereinigungsmenge soll ermittelt werden. Die Mengen A und B in aufzählender Form:

Die Vereinigungsmenge in aufzählender und beschreibender Form:
![]()
Beispiel Vereinigungsmenge:
Im vorangegangenem Beispiel zur Schnittmenge sind die Mengen F, I und D angegeben. 
Es handelt sich dabei um Schüler, die die Kurse Fotografie (F), Informatik (I) und Digitaltechnik (D) belegen. ![]()
Welche Elemente enthält dann die Vereinigungsmenge dieser drei Mengen, und wie ist diese Menge entsprechend der Aufgabe zu beschreiben? ![]()
Rechnung Vereinigungsmenge:
Die Vereinigungsmenge enthält 20 Elemente (Schüler) und zwar sind es alle Schüler der Klasse SF23S, die Kurse wählen konnten.
F ![]() I
I ![]() D = {Schüler der Klasse SF23S}
D = {Schüler der Klasse SF23S}

Vereinigungsmenge kommutativ
Ebenso wie die Schnittmengenbildung ist die Bildung der Vereinigungsmenge kommutativ.
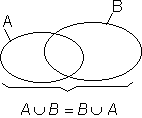 Der Nachweis erfolgt über die Mengendiagramme.
Der Nachweis erfolgt über die Mengendiagramme.
Teilmenge und Vereinigungsmenge
Ist A Teilmenge von B, so ist die Vereinigungsmenge von A und B gleich der Menge B.
![]()
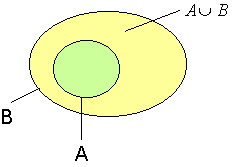
Der Beweis erfolgt wieder über die Mengenbilder.
Die leere Menge zeigt sich bezüglich der Vereinigungsmengenbildung als neutrales Element, d.h. die Vereinigung mit der leeren Menge führt zu keiner Veränderung gegenüber der Ausgangsmenge.
![]()
Definition Restmenge
Eine weitere Verknüpfung von Mengen ist auch die Restmenge. Die Restmenge A ohne B zweier Mengen A und B ist die Menge der Elemente, die in der Menge A, aber nicht in der Menge B enthalten sind.
![]()
Die Restmenge C ist die Menge A ohne die Elemente der Menge B.
C= A\B Symbol für ohne: \
Restmenge nicht kommutativ
Die Restmengenbildung ist nicht kommutativ.
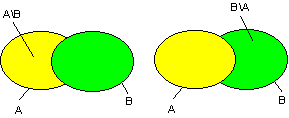
![]()
Der direkte Beweis erfolgt über die Mengenbilder.
Beispiel Restmenge:
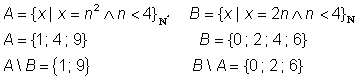
Die Produktmengenverknüpfung
Definition Paarmenge
Eine Paarmenge ist eine Menge, deren Elemente aus Wertepaaren bestehen, deren Ordnung festgelegt ist.
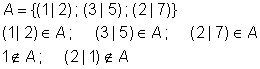
Der Begriff Ordnung bedeutet, es ist festgelegt, welche Komponente des Wertepaares an erster Stelle geschrieben wird.
![]()
Definition Produktmenge
Die Produktmenge der Mengen A und B ist die Menge aller möglichen geordneten Paare, mit der Ordnung steht an erster Stelle und steht an zweiter Stelle im Wertepaar.
![]()
Die Produktmenge zweier Mengen ist nicht kommutativ, da die Ordnung in den Elementen der beiden Mengen verschieden ist.
Beispiel Produktmenge:

Eine Übersicht über alle Mengenbegriffe und mathematischen Zeichen findest du hier.
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Aussagen und Mengen, darin auch Links zu Aufgaben.

