Hier findest du die Lösungen der Aufgaben zu ganzrationalen Funktionen I zur Vorbereitung einer Klassenarbeit, darin geht es um Nullstellen, Symmetrie etc.
1. Bedeutung?
Ausführliche Lösung
f(x) stellt eine ganzrationale Funktion n-ten Grades dar.
Der höchste Exponent n gibt den Grad der Funktion an.
![]()
2. Symmetrie
Was weißt du über die Symmetrie ganzrationaler Funktionen ?
Ausführliche Lösung
Der Graph einer ganzrationalen Funktion ist genau dann achsensymmetrisch, wenn die Funktionsgleichung nur aus geraden Exponenten besteht.
![]()
Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch, wenn die Funktionsgleichung nur aus ungeraden Exponenten besteht.
![]()
3. Symmetrieeigenschaft
Mache eine Aussage über die Symmetrieeigenschaft folgender Funktionenund begründe deine Aussage.
Ausführliche Lösung
a)
![]()
b)
![]()
c)

d)

4. Verlauf
Wodurch wird der Verlauf einer ganzrationalen Funktion bestimmt?
Ausführliche Lösung
Der Verlauf einer ganzrationalen Funktion wird durch den Summanden mit der höchsten Potenz bestimmt, also durch anxn.
5. Wie verlaufen folgende Funktionsgraphen?
Wie verlaufen folgende Funktionsgraphen?
Ausführliche Lösung
a)
![]()
b)
![]()
c)
![]()
d)
![]()
6. Nullstellen
Was weißt du über die Anzahl der Nullstellen ganzrationaler Funktionen?
Ausführliche Lösung
Eine ganzrationale Funktion n ten Grades hat höchstens n Nullstellen.
Ist der Grad n ungerade, so hat sie mindestens eine Nullstelle.
7. Welcher Art sind die Nullstellen
Berechne die Nullstellen folgender Funktionen und stelle die Funktionsgleichung als Produkt von Linearfaktoren dar. Welcher Art sind die Nullstellen (einfach, doppelt oder dreifach)
Ausführliche Lösung
a)

b)

8. Verlauf des Graphen?
Berechne die Nullstellen folgender Funktionen. Mache eine Aussage über den Verlauf des Graphen. Wohin streben die Funktionswerte für große, bzw. kleine x- Werte?
Ausführliche Lösung
a)
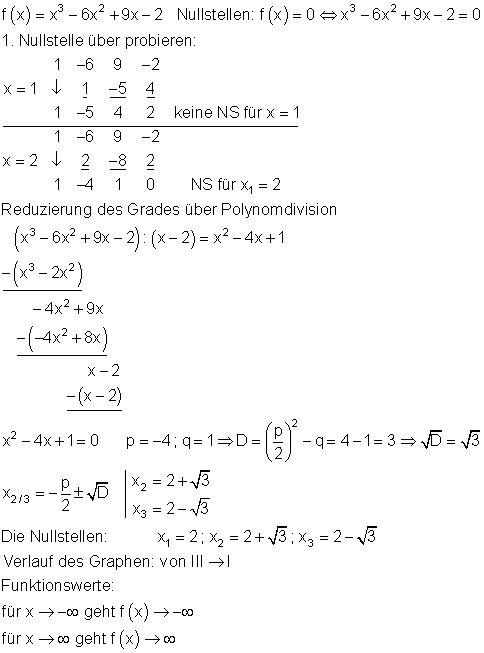
b)
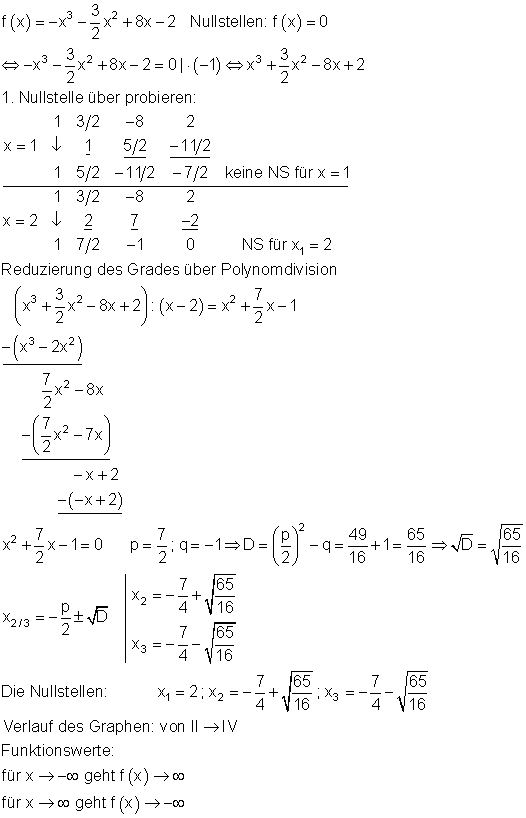
9. Hornerschema
Berechne für f(x) nach dem Hornerschema die Wertetabelle, berechne die Nullstellen und zeichne den Graphen so genau wie möglich.
Dazu kannst du dir das 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
Ausführliche Lösung
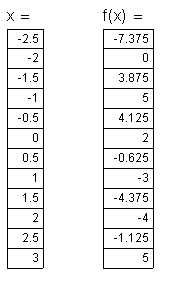
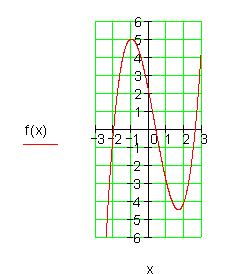
![]()
10. Ausführliche Aufgabe
Der Graph einer ganzrationalen Funktion 3. Grades geht durch die Punkte
Ausführliche Lösung
a) Die Funktionsgleichung einer ganzrationalen Funktion 3. Grades lautet:
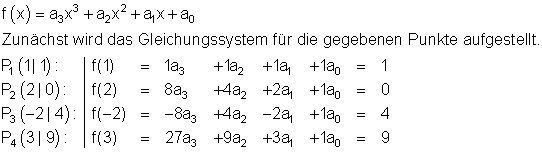
Lösung des Gleichungssystems mit dem Gauß- Algorithmus:
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.

Bestimmen der Koeffizienten durch Rückwärtseinsetzen:
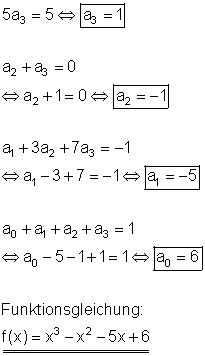
b)
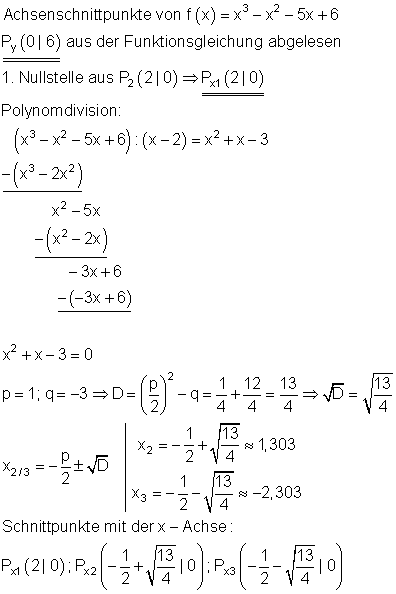
c)
Ermittele mit dem Horner-Schema die Funktionswerte für
![]()
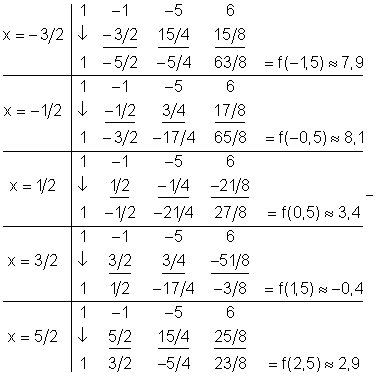
d)
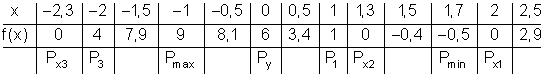
e)
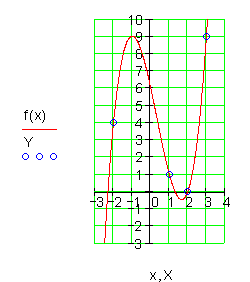
f) Der Graph verläuft von III nach I
g) Keine Symmetrie, da sowohl gerade als auch ungerade Exponenten vorkommen.
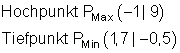
Dazu findest du hier die Aufgaben.
Und hier die dazugehörige Theorie: Zusammenfassung ganzrationale Funktionen.
Hier eine Übersicht über weitere ganzrationale Funktionen, darin Links zu weiteren Aufgaben.
