In diesem Beitrag findet ihr Lösungen der Aufgaben Polynomgleichungen VI mit Parametern. Weitere Aufgaben in diesem Bereich findet ihr unter Aufgaben Polynomgleichungen IV. Hier z. B.: Bestimme die Anzahl der Lösungen in Abhängigkeit von k! Z. B.: Für welche Werte von a hat die Gleichung eine Lösung, genau zwei oder drei Lösungen?
Dazu kannst du dir eine dieser Videos ansehen Playlist aller Videos zu Polynomgleichungen.
1. a) Berechne die Lösung folgender Gleichung!
Ausführliche Lösung
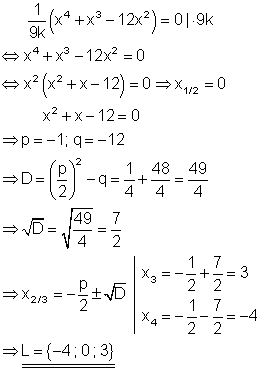
Aus der Polynomgleichung kann x2 ausgeklammert werden. Es entsteht ein Produkt. Da dieses aber Null ist, kann der Satz vom Nullprodukt angewendet werden, der da lautet:
„Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist.“
Die Lösung der Gleichung findet man also dadurch, dass man jeden Faktor für sich gleich Null setzt. Der erste Faktor ergibt die doppelte Lösung 0. Der zweite Faktor ist eine quadratische Gleichung, die mit der p-q-Formel zu lösen ist. In der Lösungsmenge erscheint die doppelte 0 nur einmal, da in der Mengendarstellung per Definition jedes Element nur einmal vorkommen darf.
1. b) Berechne die Lösung folgender Gleichung! Ausführliche Lösung
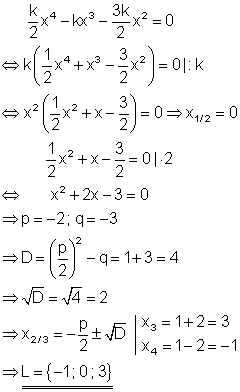
Die Polynomgleichung kann nach ausklammern von k durch k dividiert werden, da k per Definition ungleich Null ist. Damit hat k keinen Einfluss auf die Lösung. x2 lässt sich ebenfalls ausklammern, so dass die Lösungen nach dem Satz vom Nullprodukt bestimmt werden können.
1. c) Berechne die Lösung folgender Gleichung! Ausführliche Lösung
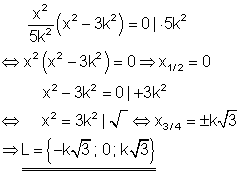
2. a) Löse die Gleichung nach x auf! Ausführliche Lösung

Die Polynomgleichung stellt eine biquadratische Gleichung dar. Die Substitutionsvariable z lässt sich mithilfe der p-q-Formel berechnen. Anschließend muss zurücksubstituiert und die Wurzel gezogen werden. Die Wurzel lässt sich nur für positive z-Werte lösen.
2. b) Löse die Gleichung nach x auf! Ausführliche Lösung
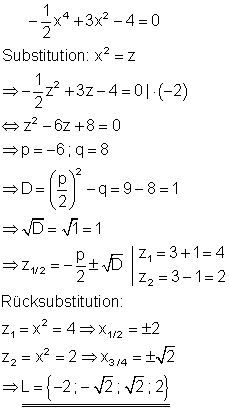
2. c) Löse die Gleichung nach x auf! Ausführliche Lösung
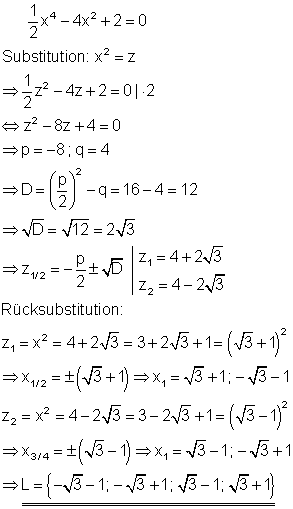
Nach der Rücksubstitution kann man den Term mit Hilfe der binomischen Formeln in ein Quadrat verwandeln, aus dem die Wurzel gezogen werden kann.
3. a) Lösen Sie die Gleichung nach x auf! Ausführliche Lösung
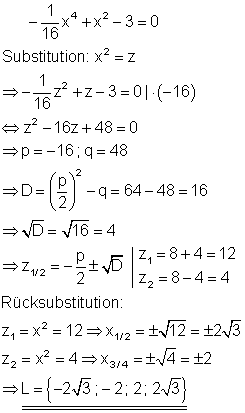
3. b) Löse die Gleichung nach x auf! Ausführliche Lösung
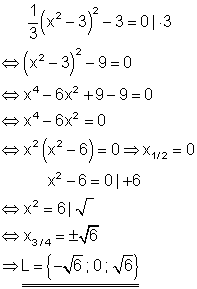
3. c) Löse die Gleichung nach x auf! Ausführliche Lösung
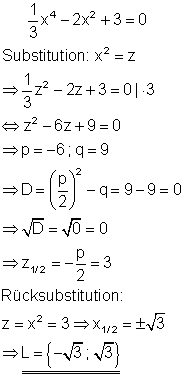
4. a) Löse die Gleichung nach x auf! Ausführliche Lösung
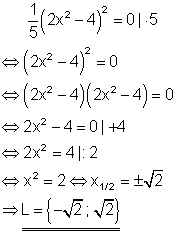
Der Term kann als Produkt zweier Faktoren geschrieben werden. Da beide Faktoren gleich sind, genügt es nur einen davon gleich Null zu setzen, da der andere Faktor die gleiche Lösung hat. Damit hat die Polynomgleichung insgesamt zwei Lösungen, die doppelt auftreten.
4. b) Löse die Gleichung nach x auf! Ausführliche Lösung
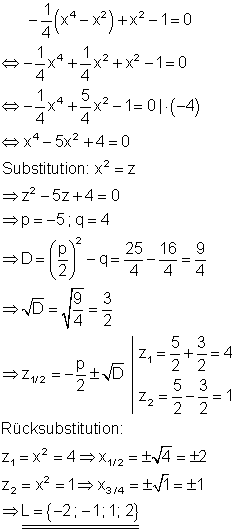
4. c) Löse die Gleichung nach x auf! Ausführliche Lösung
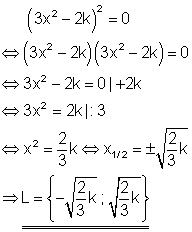
Der Term kann als Produkt zweier Faktoren geschrieben werden. Da beide Faktoren gleich sind, genügt es nur einen davon gleich Null zu setzen, da der andere Faktor die gleiche Lösung hat. Damit hat die Polynomgleichung insgesamt zwei Lösungen, die doppelt auftreten. Da per Definition die Formvariable k > 0 sein soll, gilt die Lösung für jeden Wert von k, solange er größer als Null ist.
5. a) Löse die Gleichung nach x auf! Ausführliche Lösung
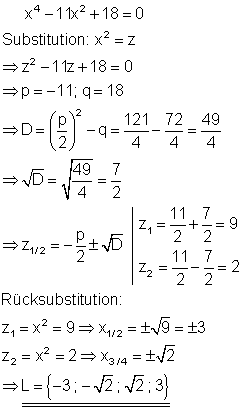
5. b) Löse die Gleichung nach x auf! Ausführliche Lösung
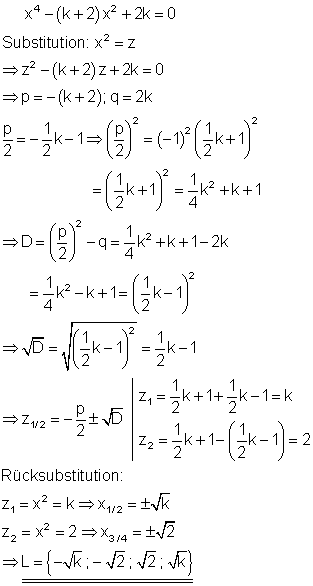
5. c) Lösen Sie die Gleichung nach x auf! Ausführliche Lösung
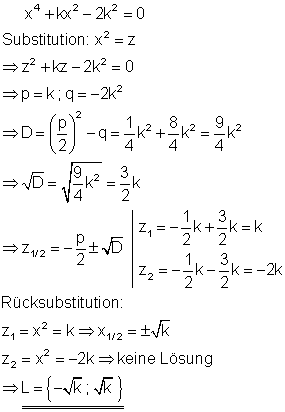
Es gibt für die Polynomgleichung nur zwei Lösungen. Für z2 = -2k gibt es keine Lösung, da der Wert für alle k > 0 negativ ist. Aus einer negativen Zahl lässt sich keine Wurzel ziehen.
6. Für welchen Wert von k hat die Gleichung
![]()
Berechne für diesen Fall die weiteren Lösungen! Ausführliche Lösung
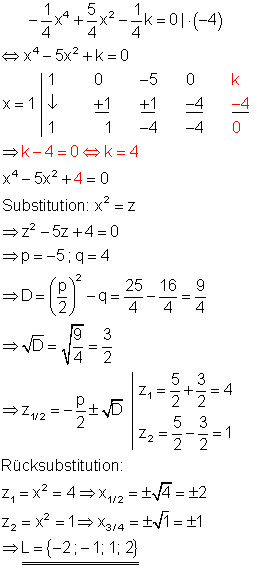
Da die Lösung x = 1 bekannt ist, kann man mit dem Horner-Schema den Wert für k bestimmenn. Die letzte Spalte im Horner-Schema muss in der Addition Null ergeben, damit x = 1 Lösung der Polynomgleichung ist. Aus der Addition ergibt sich für k der Wert k = 4. Setzt man für k die 4 in die Polynomgleichung ein, kann man sie als biquadratische Gleichung lösen.
Dazu kannst du dir das 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
7. Für welchen Wert von k hat die Gleichung
![]()
Berechne für diesen Fall die weiteren Lösungen!
Ausführliche Lösung
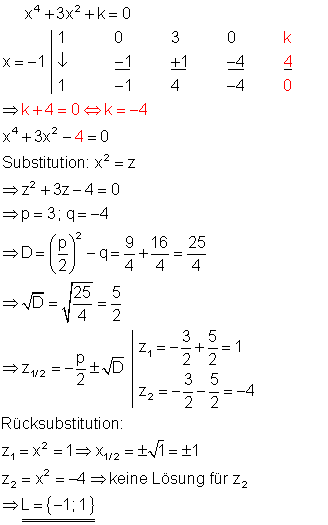
8. Zeige
![]()
Ausführliche Lösung
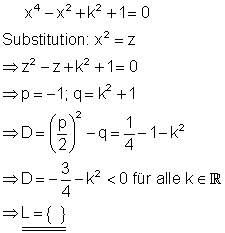
Die Diskriminante D ist für jeden Wert von k negativ, da k als Quadrat auftritt.
Wenn die Gleichung in z keine Lösung hat, dann hat sie auch keine in x.
9. Löse auf
![]()
Ausführliche Lösung
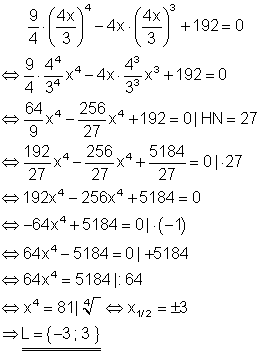
10. Für welche Werte von k
![]() Ausführliche Lösung
Ausführliche Lösung
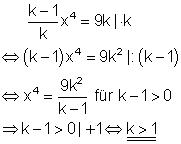
Der Nenner des Bruches darf nicht 0 werden. Damit scheidet k = 1 aus. Weiterhin darf der Bruch nicht negativ werden, denn die 4. Wurzel ist nur für positive Zahlen definiert. Der Zähler ist wegen k2 immer positiv. Damit der Bruch positiv ist, muss k > 1 sein.
11. Bestimme
![]()
Bestimme die Anzahl der Lösungen in Abhängigkeit von k!
Ausführliche Lösung
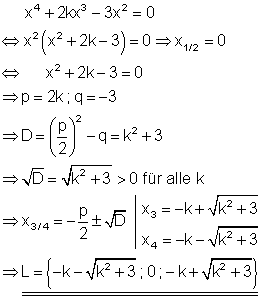
Es gibt für alle Werte von k immer 3 Lösungen.
12. Gib eine Gleichung 4. Grades an,
die jeweils vier, drei, zwei bzw. eine Lösung besitzt!
Ausführliche Lösung
Die Kombination von Linearfaktoren liefert die jeweils gewünschte Gleichung.
Vier Lösungen:
4. Lösung:
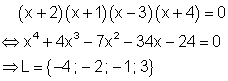
3. Lösungen:
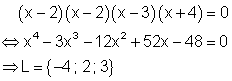
2. Lösungen:
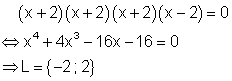
1. Lösung:
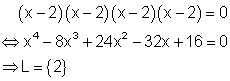
Hier findest du die Aufgaben.
Und hier weitere Aufgaben Polynomgleichungen V Text- und Parameteraufgaben.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.
